
| A. | ($\frac{1}{9}$,9) | B. | [$\frac{1}{9}$,9] | C. | (0,$\frac{1}{9}$]∪[9,+∞) | D. | (0,$\frac{1}{9}$)∪(9,+∞) |
分析 要使函数f(x)=$\frac{2x+1}{\sqrt{(lo{g}_{3}x)^{2}-4}}$有意义,只需$\left\{\begin{array}{l}{x>0}\\{(lo{g}_{3}x)^{2}-4>0}\end{array}\right.$,解不等式即可得到所求定义域.
解答 解:要使函数f(x)=$\frac{2x+1}{\sqrt{(lo{g}_{3}x)^{2}-4}}$有意义,
只需$\left\{\begin{array}{l}{x>0}\\{(lo{g}_{3}x)^{2}-4>0}\end{array}\right.$,
即$\left\{\begin{array}{l}{x>0}\\{lo{g}_{3}x<-2或lo{g}_{3}x>2}\end{array}\right.$,
即有$\left\{\begin{array}{l}{x>0}\\{x<\frac{1}{9}或x>9}\end{array}\right.$,
则x>9或0<x<$\frac{1}{9}$.
定义域为(0,$\frac{1}{9}$)∪(9,+∞).
故选:D.
点评 本题考查函数的定义域的求法,注意运用分式分母不为0,偶次根式被开方式非负,以及对数函数的真数大于0,考查运算能力,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 0<b<1 | B. | b<0 | C. | -2<b<0 | D. | -1<b<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{2}$ | B. | $\frac{11}{2}$ | C. | 6 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y={log_a}{x^2}$与y=2logax | B. | y=2x与$y={log_a}{a^{2x}}$ | ||
| C. | $y=\sqrt{{x^2}-4}$与$y=\sqrt{x+2}•\sqrt{x-2}$ | D. | $y=\sqrt{x^2}$与y=x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
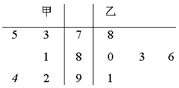 甲、乙两名选手参加歌手大赛时,5名评委打的分数用茎叶图表示(如图).s1、s2分别表示甲、乙选手分数的标准差,则s1与s2的关系是( )
甲、乙两名选手参加歌手大赛时,5名评委打的分数用茎叶图表示(如图).s1、s2分别表示甲、乙选手分数的标准差,则s1与s2的关系是( )| A. | s1>s2 | B. | s1=s2 | C. | s1<s2 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届江西吉安一中高三上学期段考一数学(文)试卷(解析版) 题型:选择题
已知椭圆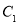 与双曲线
与双曲线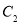 有相同的焦点
有相同的焦点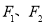 ,点
,点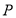 是
是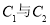 的一个公共点,
的一个公共点,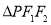 是以一个以
是以一个以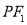 为底的等腰三角形,
为底的等腰三角形,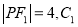 的离心率为
的离心率为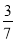 ,则
,则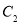 的离心率是( )
的离心率是( )
A.2 B.3 C. D.
D.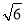
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com