练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
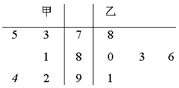
    12．甲、乙两名选手参加歌手大赛时，5名评委打的分数用茎叶图表示（如图）．s1、s2分别表示甲、乙选手分数的标准差，则s1与s2的关系是（　　）
    A．s1＞s2B．s1=s2C．s1＜s2D．不确定

    分析 根据平均数与方差、标准差的意义进行判断即可．

    解答 解：甲选手的平均分是$\overline{{x}_{1}}$=$\frac{1}{5}$×（73+75+81+92+94）=83，
    乙选手的平均分是$\overline{{x}_{2}}$=$\frac{1}{5}$×（78+80+83+86+91）=83.6，
    这两个选手的平均分是基本相同的，
    从茎叶图上看甲的分数是双峰的，分布较分散，
    乙的分数是单峰的，分布较集中，
    所以甲的方差大于乙的方差，即甲的标准差大于乙的标准差．
    故选：A．

    点评 本题考查了茎叶图的应用问题，也考查了从茎叶图中观察两组数据的波动大小，判断方差、标准差的问题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

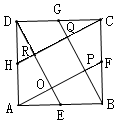    4．如图，边长为2的正方形ABCD的四边中点E、F、G、H分别与D、A、B、C四点相连，其交点分别为O、P、Q、R，那么四边形OPQR的面积为（　　）
    A．$\frac{1}{4}$B．$\frac{1}{5}$C．$\frac{2}{5}$D．$\frac{4}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．若A⊆{1，2，3}则满足条件的集合A的个数是（　　）
    A．8B．7C．6D．9

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．设f（x）=$\left\{\begin{array}{l}{x^2}-1，x＜2\\ 3x，x≥2\end{array}$，则f（f（-2））的值为（　　）
    A．3B．6C．9D．12

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．函数f（x）=$\frac{2x+1}{\sqrt{（lo{g}_{3}x）^{2}-4}}$的定义域为（　　）
    A．（$\frac{1}{9}$，9）B．[$\frac{1}{9}$，9]C．（0，$\frac{1}{9}$]∪[9，+∞）D．（0，$\frac{1}{9}$）∪（9，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．①若椭圆$\frac{x^2}{25}$+$\frac{y^2}{16}$=1的左右焦点分别为F1、F2，动点P满足|PF1|+|PF2|＞10，则动点P不一定在该椭圆外部；
    ②椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的离心率e=$\frac{{\sqrt{2}}}{2}$，则b=c（c为半焦距）；
    ③双曲线$\frac{x^2}{25}$-$\frac{y^2}{9}$=1与椭圆$\frac{x^2}{35}$+y2=1有相同的焦点；
    ④抛物线y2=4x上动点P到其焦点的距离的最小值为1．
    其中真命题的序号为②③④．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的表面积为96+4（$\sqrt{2}$-1）π．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．已知f（x）=-x2+4x，x∈[0，2]，则函数的值域是[0，4]．

    查看答案和解析>>

    科目：高中数学 来源：2017届江西吉安一中高三上学期段考一数学（文）试卷（解析版） 题型：选择题

    已知数列是等比数列，若，则等于（ ）

    A．8 B．-8 C．16 D．-16

    查看答案和解析>>

    同步练习册答案