
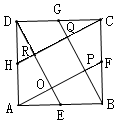
 如图,边长为2的正方形ABCD的四边中点E、F、G、H分别与D、A、B、C四点相连,其交点分别为O、P、Q、R,那么四边形OPQR的面积为( )
如图,边长为2的正方形ABCD的四边中点E、F、G、H分别与D、A、B、C四点相连,其交点分别为O、P、Q、R,那么四边形OPQR的面积为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{5}$ |
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 0<b<1 | B. | b<0 | C. | -2<b<0 | D. | -1<b<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
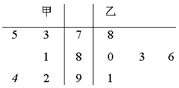 甲、乙两名选手参加歌手大赛时,5名评委打的分数用茎叶图表示(如图).s1、s2分别表示甲、乙选手分数的标准差,则s1与s2的关系是( )
甲、乙两名选手参加歌手大赛时,5名评委打的分数用茎叶图表示(如图).s1、s2分别表示甲、乙选手分数的标准差,则s1与s2的关系是( )| A. | s1>s2 | B. | s1=s2 | C. | s1<s2 | D. | 不确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com