
分析 可设出对称的两个点P,Q的坐标,利用两点关于直线x+y=0成轴对称,可以设直线PQ的方程为y=x+b,由于P、Q两点存在,可得方程组$\left\{\begin{array}{l}{y=a{x}^{2}-1}\\{y=x+b}\end{array}\right.$,有两组不同的实数解,利用中点在直线上消去参数b,建立关于a的函数关系,求出变量a的范围.
解答 解:设抛物线上关于直线l对称的两相异点为P(x1,y1)、Q(x2,y2),线段PQ的中点为M(x0,y0),
设直线PQ的方程为y=x+b,由于P、Q两点存在,
∴$\left\{\begin{array}{l}{y=a{x}^{2}-1}\\{y=x+b}\end{array}\right.$,有两组不同的实数解,即得方程ax2-x-(1+b)=0有两个解.①
∵△=1+4a(1+b)>0.②
x1+x2=$\frac{1}{a}$,
由中点坐标公式可得,x0=$\frac{{x}_{1}+{x}_{2}}{2}$=$\frac{1}{2a}$,y0=x0+b=$\frac{1}{2a}$+b.
∵M在直线L上,
∴0=x0+y0=$\frac{1}{2a}$+$\frac{1}{2a}$+b,
即b=-$\frac{1}{a}$,代入②解得a>$\frac{3}{4}$.
故实数a的取值范围($\frac{3}{4}$,+∞)
故答案为:($\frac{3}{4}$,+∞).
点评 本题考查了直线与抛物线的位置关系,以及对称问题,考查方程的根与系数关系及方程思想的应用,属于中档题


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | M∩N | B. | M∩(∁UN) | C. | (∁UM)∩N | D. | (∁UM)∩(∁UN) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)是奇函数,g(x)是偶函数 | B. | f(x)是偶函数,g(x)是奇函数 | ||
| C. | f(x)和g(x)都是偶函数 | D. | f(x)和g(x)都是奇函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
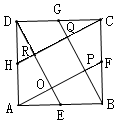 如图,边长为2的正方形ABCD的四边中点E、F、G、H分别与D、A、B、C四点相连,其交点分别为O、P、Q、R,那么四边形OPQR的面积为( )
如图,边长为2的正方形ABCD的四边中点E、F、G、H分别与D、A、B、C四点相连,其交点分别为O、P、Q、R,那么四边形OPQR的面积为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相交 | B. | 相切或相离 | C. | 相离 | D. | 相交或相切 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com