
分析 利用辅助角和两角和与差的余弦函数对已知函数式进行变形,求得sinφ、cosφ的值.然后根据同角三角函数关系进行解答.
解答 解:∵12cosθ-5sinθ=13($\frac{12}{13}$cosθ-$\frac{5}{13}$sinθ)=13(cosφcosθ-sinφsinθ)=Acos(θ+φ)(A>0),
∴cosφ=$\frac{12}{13}$,sinφ=$\frac{5}{13}$,
∴tanφ=$\frac{sinφ}{cosφ}$=$\frac{\frac{5}{13}}{\frac{12}{13}}$=$\frac{5}{12}$.
故答案是:$\frac{5}{12}$.
点评 本题考查两角和与差的三角函数,同角三角函数关系式的应用,属于基本知识的考查.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | f(x)是奇函数,g(x)是偶函数 | B. | f(x)是偶函数,g(x)是奇函数 | ||
| C. | f(x)和g(x)都是偶函数 | D. | f(x)和g(x)都是奇函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
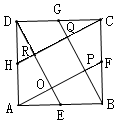 如图,边长为2的正方形ABCD的四边中点E、F、G、H分别与D、A、B、C四点相连,其交点分别为O、P、Q、R,那么四边形OPQR的面积为( )
如图,边长为2的正方形ABCD的四边中点E、F、G、H分别与D、A、B、C四点相连,其交点分别为O、P、Q、R,那么四边形OPQR的面积为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相交 | B. | 相切或相离 | C. | 相离 | D. | 相交或相切 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 增函数 | B. | 先增后减函数 | C. | 减函数 | D. | 先减后增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com