
分析 (1)(2)化解集合A,确定其元素范围,根据集合的并集、交集及其基本运算求解m的范围即可.
解答 解:(1)由题意得:集合A={x|x2-3x-10≤0}={x|-2≤x≤5},B={x|m-4≤x≤3m+2}.
∵A∪B=B,
∴A⊆B,
∴有$\left\{\begin{array}{l}m-4≤-2\\ 3m+2≥5\end{array}\right.$,
解得:1≤m≤2.
所以A∪B=B时,实数m的取值范围是[1,2].
(2)由(1)可知A={x|-2≤x≤5},B={x|m-4≤x≤3m+2}.
∵A∩B=B,
∴B⊆A,
①当B=∅时,满足题意,此时m-4>3m+2,
解得:m<-3;
②当B≠∅时,要使B⊆A,需满足:$\left\{\begin{array}{l}m-4≤3m+2\\ m-4≥-2\\ 3m+2≤5\end{array}\right.$,不等式无解;
综上可得,m<-3.
所以A∩B=B时,实数m的取值范围是(-∞,-3).
点评 本题考查了并集,交集及其运算,考查了一元二次不等式的解法,是基础题.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 4 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{2}$ | B. | $\frac{11}{2}$ | C. | 6 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y={log_a}{x^2}$与y=2logax | B. | y=2x与$y={log_a}{a^{2x}}$ | ||
| C. | $y=\sqrt{{x^2}-4}$与$y=\sqrt{x+2}•\sqrt{x-2}$ | D. | $y=\sqrt{x^2}$与y=x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源:2017届山东临沭一中高三上学期10月月考数学(文)试卷(解析版) 题型:选择题
在等差数列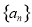 中,已知
中,已知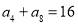 ,则该数列前
,则该数列前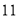 项和
项和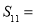 ( )
( )
A.58 B.88 C.143 D.176
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com