��������{an}����������{an+1-an}Ϊ{an}�ġ������С���
��I����{an}�ġ������С���һ�����Ϊ��ĵȲ����У���д��{an}��һ��ͨ�ʽ��
��II����a1=2��{an}�ġ������С���ͨ��Ϊ2n��������{an}��ǰn���Sn��
��III�����ڣ�II���е�����{an}��������{bn}����anbnbn+1=-21•28��n��N*������b4=-7��
������{bn}��ͨ�ʽ���ڵ�����{bn}ǰn��Ļ����ʱn��ֵ��
���𰸡�
��������1����������д�����������ʽ�ӣ�
��2���������{a
n}�ǹ�����Ϊ2�ĵȱ����У����������{a
n}��ǰn���S
n
��3������������������{b
n}��ͨ�ʽ�����������{b
n}ǰn��Ļ�ΪT
n��������{b
n}ǰn��Ļ����ʱn��ֵ��
����⣺������a
n=n
2�����𰸲�Ωһ�����ӦΪa
n=An
2+Bn+C����ʽ������A��0����3�֣�
����������a
n+1-a
n=2
n��n=1��2��3��
����a
n=��a
n-a
n-1��+��a
n-1-a
n-2��+��a
n-2-a
n-3��++��a
2-a
1��+a
1=2
n-1+2
n-2+2
n-3++2=2
n����5�֣�
����{a
n}�ǹ�����Ϊ2�ĵȱ����У�
����
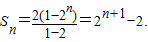
��7�֣�
������a
nb
nb
n+1=-21•2
n��a
n-1b
n-1b
n=-21•2
n����ʽ�����
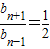
��
��������{b
2n-1}��{b
2n}�ֱ��ǹ���Ϊ

�ĵȱ�����
��b
4=-7��b
2=-14��
��n=1����a
1b
1b
2=-21•2
n��b
1=3•2
6��
��������{b
n}��ͨ��Ϊ

��10�֣�
�ڼ�����{b
n}ǰn��Ļ�ΪT
n��
��

��
��
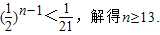
���Ե�n������ʱ��|b
1b
2|��1��|b
3b
4|��1����|b
11b
12|��1��|b
13b
14|��1��|b
15b
16|��1��
�Ӷ�|T
2|��|T
4|��|T
12|��|T
12|��|T
14|����
��n��ż��ʱ��|b
2b
3|��1��|b
4b
5|��1����|b
12b
13|��1��|b
14b
15|��1��|b
16b
17|��1��
�Ӷ�|T
1|��|T
3|��|T
13|��|T
13|��|T
15|��
ע�T
12��0��T
13��0����T
13=b
13T
12=3T
12��T
12��
���Ե�����{b
n}ǰn��Ļ�T
n���ʱn=13����14�֣�
������������Ҫ��������ͨ�ʽ����⼰ǰn�������⣮

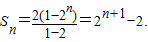 ��7�֣�
��7�֣�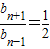 ��
�� �ĵȱ�����
�ĵȱ����� ��10�֣�
��10�֣� ��
��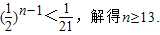


 �����������Ů��ͯ������ϵ�д�
�����������Ů��ͯ������ϵ�д�
 ������{an}����an+1=H��an����n��N*������a1�ʣ�0��1�������ж�an+1��an�Ĵ�С����֤��֮��
������{an}����an+1=H��an����n��N*������a1�ʣ�0��1�������ж�an+1��an�Ĵ�С����֤��֮�� ������{an}����an+1=H��an����n��N*������a1�ʣ�0��1�������ж�an+1��an�Ĵ�С����֤��֮��
������{an}����an+1=H��an����n��N*������a1�ʣ�0��1�������ж�an+1��an�Ĵ�С����֤��֮��