
设二次函数f(x)=x2+ax+a,方程f(x)-x=0的两根x1和x2满足0<x1<x2<1.
(1)求实数a的取值范围;
(2)试比较f(0)·f(1)-f(0)与的大小,并说明理由
(1)令g(x)=f(x)-x=x2+(a-1)x+a,
则由题意可得
?
?0
(2)f·f-f=gg=2a2,令h(a)=2a2,
∵当a>0时,h(a)单调递增,∴当0
=2·<,即f·f-f<.
法二:同解法一.
∵ff-f=gg=2a2,由知
0
2a2-=(32a2-1)=(4a-1)(4a+1)<0,
即2a2-<0,故ff-f<.
法三:方程f(x)-x=0?x2+(a-1)x+a=0,由韦达定理得x1+x2=1-a,x1x2=a,于是0
??
?0
依题意可设g(x)=(x-x1)(x-x2),则由0


科目:高中数学 来源:浙江省杭州高中2006-2007学年度第一学期高三年级第三次月考 数学试题(文) 题型:044
| |||||||||||||||
查看答案和解析>>
科目:高中数学 来源:学习周报 数学 人教课标高一版(A必修2) 2009-2010学年 第26期 总182期 人教课标高一版 题型:044
设二次函数f(x)=x2+2x+b的图象与两坐标轴有三个交点,经过这三个交点的圆记为圆C.
(1)求实数b的取值范围;
(2)求圆C的方程;
(3)问圆C是否经过某定点(其坐标与b无关)?若是,求出定点的坐标;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源:2014届云南省高一下学期期末数学试卷(解析版) 题型:解答题
(12分)(1)设x、y、z R,且x+y+z=1,求证x2+y2+z2≥
R,且x+y+z=1,求证x2+y2+z2≥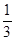 ;
;
(2)设二次函数f (x)=ax2+bx+c (a>0),方程f (x)-x=0有两个实根x1,x2,
且满足:0<x1<x2< ,若x
,若x (0,x1)。
(0,x1)。
求证:x<f (x)<x1
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)当x∈(0,x1)时,证明x<f(x)<x1;
(2)设函数f(x)的图象关于直线x=x0对称;
证明:x0<![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com