已知
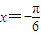
是方程
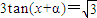
的一个解,α∈(-π,0),则α=
.
【答案】
分析:先将
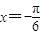
代入求出tan(-
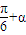
)的值,再由正切函数的性质可得到α的值,最后根据α的范围确定最后答案.
解答:解:将
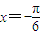
代入
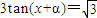
得3tan(-
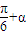
)=
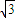
∴tan(-
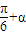
)=

∴-
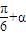
=

∴α=
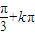
,又∵α∈(-π,0),
故答案为:-
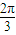 点评:
点评:本题主要考查正切函数的基本性质.属基础题.
练习册系列答案
相关习题
科目:高中数学
来源:2012年江苏省四星高中高三数学小题训练(11)(解析版)
题型:解答题
已知

是方程

的一个解,α∈(-π,0),则α=
.
查看答案和解析>>
科目:高中数学
来源:2010年上海市崇明县高考数学一模试卷(理科)(解析版)
题型:解答题
已知
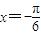
是方程
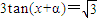
的一个解,α∈(-π,0),则α=
.
查看答案和解析>>
科目:高中数学
来源:2010年上海市崇明县高考数学一模试卷(文科)(解析版)
题型:解答题
已知
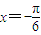
是方程
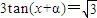
的一个解,α∈(-π,0),则α=
.
查看答案和解析>>
科目:高中数学
来源:2011年江苏省苏北四市四星级重点高中高三联考数学试卷(文科)(解析版)
题型:解答题
已知
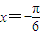
是方程
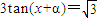
的一个解,α∈(-π,0),则α=
.
查看答案和解析>>
科目:高中数学
来源:2010年江苏省宿迁市高考数学模拟试卷(四)(解析版)
题型:解答题
已知
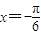
是方程
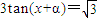
的一个解,α∈(-π,0),则α=
.
查看答案和解析>>

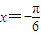 是方程
是方程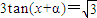 的一个解,α∈(-π,0),则α= .
的一个解,α∈(-π,0),则α= .