
如右图 ,A、B、C、D为空间四点.在△ABC中,AB=2,AC=BC=.等边三角形ADB以AB为轴运动.
,A、B、C、D为空间四点.在△ABC中,AB=2,AC=BC=.等边三角形ADB以AB为轴运动.
(1)当平面ADB⊥平面ABC时,求CD;
(2)当△ADB转动时,是否总有AB⊥CD?
证明你的结论.
(1)取AB的中点E,连结DE,CE,
因为ADB是等边三角形,所以DE⊥AB.
当平面ADB⊥平面ABC时,
因为平面ADB∩平面ABC=AB,
所以DE⊥平面ABC,可知DE⊥CE,
由已知可得DE=,EC=1,
在Rt△DEC中,CD==2.
(2)当△ADB以AB为轴转动时,总有AB⊥CD.
证明:①当D在平面ABC内时,因为AC=BC,AD=BD,所以C,D都在线段AB的垂直平分线上,即AB⊥CD.
②当D不在平面ABC内时,由(1)知AB⊥DE.又因AC=BC,所以AB⊥CE.
又DE,CE为相交直线,
所以AB⊥平面CDE,由CD⊂平面CDE,得AB⊥CD.
综上所述,总有AB⊥CD.
【解析】略


科目:高中数学 来源:高中数学综合题 题型:013
如右图,A、B、C、D是某煤矿的四个采煤点,l是公路,图中所标线段为道路,ABQP、BCRQ、CDSR近似于正方形.已知A、B、C、D四个采煤点每天的采煤量之比约为5∶1∶2∶3,运煤的费用与运煤的路程、所运煤的重量都成正比.现要从P、Q、R、S中选出一处设立一个运煤中转站,使四个采煤点的煤运到中转站的费用最少,则地点应选在
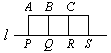
[ ]
A.P点 B.R点 C.Q点 D.S点
查看答案和解析>>
科目:高中数学 来源: 题型:
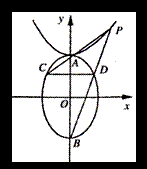
如右图,A、B分别是椭圆![]() 的上、下两顶点,P是双曲线
的上、下两顶点,P是双曲线
![]() 上在第一象限内的一点,直线PA、PB分别交椭圆于C、D点,如果D恰
上在第一象限内的一点,直线PA、PB分别交椭圆于C、D点,如果D恰
是PB 的中点.
(1)求证:无论常数a、b如何,直线CD的斜率恒为定值;
(2)求双曲线的离心率,使CD通过椭圆的上焦点.
查看答案和解析>>
科目:高中数学 来源:2013届吉林长春市高二第二次月考文科数学试卷(解析版) 题型:选择题
如右图,A、B是⊙O上的两点,AC是⊙O的切线,∠B=70°,则∠BAC等于

A. 70° B. 35° C. 20° D. 10°
查看答案和解析>>
科目:高中数学 来源:新课标高三数学空间向量及其运算、角的概念及其求法和空间距离专项训练(河北) 题型:选择题
一个正方体的展开图如右图所示,B,C,D为原正方体的顶点,A为原正方体一条棱的中点.在原来的正方体中,CD与AB所成角的余弦值为 ( )
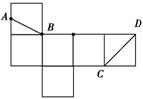 A. B.
A. B.
C. D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com