
如图,平面a∥平面b,A、B∈a,C∈b,AAˊ⊥b于Aˊ,BBˊ⊥b于Bˊ,若AC⊥AB,AC与bb成60°的角,AC=8cm,BˊC=6cm,求异面直线AC与BBˊ间的距离.
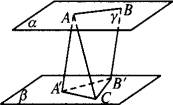
解:∵AAˊ⊥b于Aˊ,BBˊ⊥b于Bˊ, 且AˊBˊ ∴AAˊ和BBˊ可确定一平面,设为γ,且γ∩a=AB,γ∩b=AˊBˊ.∵a∥b,∴AB∥AˊBˊ. 又∵AB⊥AC,AˊBˊ⊥AC.又∵AAˊ⊥b.∴AˊBˊ⊥AˊC. 由AAˊ⊥AˊBˊ,AAˊ∩AˊC=Aˊ,∴AˊBˊ⊥平面AˊAC. 由AAˊ∥BBˊ,∴BBˊ∥平面AAˊC. ∴BBˊ与AC间的距离为BBˊ与平面AAˊC间的距离.由 AˊBˊ⊥平面AˊAC.∴BBˊ与AC间的距离为AˊBˊ的长. 由AAˊ⊥b,AC=8 cm,∴∠ACAˊ=60°∴AˊC=4 cm. 又∵BˊC=6cm,∴AˊBˊ=2 即异面直线AC和BBˊ间的距离为2
|


科目:高中数学 来源:数学教研室 题型:044
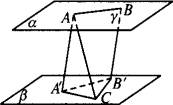
查看答案和解析>>
科目:高中数学 来源: 题型:
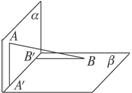
A.2∶1 B.3∶
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com