练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】给定两个命题，P：对任意实数x都有ax2+ax+1＞0恒成立；Q：关于x的方程x2﹣x+a=0有实数根；如果P与Q中有且仅有一个为真命题，求实数a的取值范围．

    【答案】

    【解析】试题分析：本题以命题的形式考察了一元二次不等式与其方程实根的问题，命题是真命题，即a＝0或，若命题是真命题，，若仅有一个为真命题，即一真一假，所以分别计算真假，或假真的不等式，求的取值范围.

    试题解析：对任意实数x都有ax2＋ax＋1＞0恒成立a＝0或0≤a＜4；

    关于x的方程x2－x＋a＝0有实数根1－4a≥0a≤；

    如果p真，且q假，有0≤a＜4，且a＞，∴＜a＜4；

    如果q真，且p假，有a＜0或a≥4，且a≤，∴a＜0.

    综上，实数a的取值范围为（－∞，0）∪.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知f（x）=sin2（π+x）﹣cos（2π﹣x）+a
    （1）求f（x）的值域
    （2）若f（x）在（0， ）内有零点，求a的范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=4cosωxsin（ωx+ ）（ω＞0）的最小正周期为π．
    （1）求ω的值；
    （2）讨论f（x）在区间[0， ]上的单调性；
    （3）当x∈[0， ]时，关于x的方程f（x）=a 恰有两个不同的解，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=2sinx（sinx+ cosx）﹣1（其中x∈R），求：
    （1）函数f（x）的最小正周期；
    （2）函数f（x）的单调减区间；
    （3）函数f（x）图象的对称轴和对称中心．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在某校组织的“共筑中国梦”竞赛活动中，甲、乙两班各有6名选手参赛，在第一轮笔试环节中，评委将他们的笔试成绩作为样本数据，绘制成如图所示的茎叶图，为了增加结果的神秘感，主持人故意没有给出甲、乙两班最后一位选手的成绩，只是告诉大家，如果某位选手的成绩高于90分（不含90分），则直接“晋级”.

    （1）求乙班总分超过甲班的概率；

    （2）主持人最后宣布：甲班第六位选手的得分是90分，乙班第六位选手的得分是97分.若主持人从甲乙两班所有选手成绩中分别随机抽取2个，记抽取到“晋级”选手的总人数为，求的分布列及数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率为，以原点为圆心，椭圆的短半轴长为半径的圆与直线x﹣y+=0相切．

    （Ⅰ）求椭圆C的方程；

    （Ⅱ）若过点M（2，0）的直线与椭圆C相交于两点A，B，当时，求直线斜率的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】我国古代数学名著《算法统宗》中有如下问题：“远望巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯？”意思是：一座7层塔共挂了381盏灯，且相邻两层中的下一层灯数是上一层灯数的2倍，则塔的顶层共有灯（ ）

    A. 1盏 B. 3盏 C. 5盏 D. 9盏

    查看答案和解析>>

    科目：高中数学 来源： 题型：

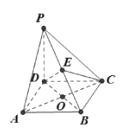
    【题目】如图，在四棱锥中， 平面，四边形是菱形， ， ，且， 交于点， 是上任意一点.

    （1）求证： ；

    （2）已知二面角的余弦值为，若为的中点，求与平面所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在数列{an}中，a1=1，an+1=2an+2n ．
    （1）设bn= ，证明：数列{bn}是等差数列．
    （2）求数列{an}的前n项和．

    查看答案和解析>>

    同步练习册答案