
【题目】一个酒杯的轴截面是一条抛物线的一部分,它的方程是x2=2y,y∈[0,10],在杯内放入一个清洁球,要求清洁球能擦净酒杯的最底部(如图),则清洁球的最大半径为 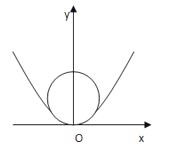
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 在(1,+∞)上是增函数,且a>0.
在(1,+∞)上是增函数,且a>0.
(Ⅰ)求a的取值范围;
(Ⅱ)求函数g(x)=ln(1+x)﹣x在[0,+∞)上的最大值;
(Ⅲ)已知a>1,b>0,证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应:
X | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
(1)求回归直线方程.
(2)回归直线必经过的一点是哪一点?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品特约经销商根据以往当地的需求情况,得出如图该种产品日需求量的频率分布直方图. 
(1)求图中a的值,并估计日需求量的众数;
(2)某日,经销商购进130件该种产品,根据近期市场行情,当天每售出1件能获利30元,未售出的部分,每件亏损20元.设当天的需求量为x件(100≤x≤150),纯利润为S元.
(ⅰ)将S表示为x的函数;
(ⅱ)根据直方图估计当天纯利润S不少于3400元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三点O(0,0),A(﹣2,1),B(2,1),曲线C上任意一点M(x,y)满足| ![]() +
+ ![]() |=
|= ![]() (
( ![]() +
+ ![]() )+2.
)+2.
(1)求曲线C的方程;
(2)动点Q(x0 , y0)(﹣2<x0<2)在曲线C上,曲线C在点Q处的切线为直线l:是否存在定点P(0,t)(t<0),使得l与PA,PB都相交,交点分别为D,E,且△QAB与△PDE的面积之比是常数?若存在,求t的值.若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合S={x|x>1},T={x||x﹣1|≤2},则(RS)∪T( )
A.(﹣∞,3]
B.[﹣1,1]
C.[﹣1,3]
D.[﹣1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}中a1=3,其前n项和Sn满足Sn=pan+1﹣ ![]() (p为非零实数)
(p为非零实数)
(1)求p值及数列{an}的通项公式;
(2)设{bn}是公差为3的等差数列,b1=1.现将数列{an}中的ab1 , ab2 , …abn…抽去,余下项按原有顺序组成一新数列{cn},试求数列{cn}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com