
【题目】已知等比数列{an}中a1=3,其前n项和Sn满足Sn=pan+1﹣ ![]() (p为非零实数)
(p为非零实数)
(1)求p值及数列{an}的通项公式;
(2)设{bn}是公差为3的等差数列,b1=1.现将数列{an}中的ab1 , ab2 , …abn…抽去,余下项按原有顺序组成一新数列{cn},试求数列{cn}的前n项和Tn .
【答案】
(1)解:依题意,等比数列{an}的公比q≠1,则Sn= ![]() =
= ![]() ,
,
∴a1﹣an+1=(1﹣q)(pan+1﹣ ![]() ),
),
整理得:a1=﹣ ![]() (1﹣q)、p(q﹣1)=1,
(1﹣q)、p(q﹣1)=1,
又∵a1=3,
∴q=3,p= ![]() ,
,
∴数列{an}的通项公式an=3n;
(2)解:∵数列{bn}是公差为3的等差数列、b1=1,
∴bn=1+3(n﹣1)=3n﹣2,
记dn= ![]() ,则dn=33n﹣2=327n﹣1,
,则dn=33n﹣2=327n﹣1,
即数列{dn}是首项为3、公比为27的等比数列,
∴Tn=Sn﹣D( ![]() )=
)= ![]() 3n+1﹣
3n+1﹣ ![]() +
+ ![]() ﹣
﹣ ![]() 27m=
27m= ![]() 3n+1﹣
3n+1﹣ ![]() ﹣
﹣ ![]() 27m,
27m,
其中( ![]() )表示
)表示 ![]() 的整数部分且记为m,D(n)表示数列{dn}的前n项和
的整数部分且记为m,D(n)表示数列{dn}的前n项和
【解析】(1)通过等比数列的求和公式及Sn=pan+1﹣ ![]() 可知q=3、p=
可知q=3、p= ![]() ,进而计算可得结论;(2)通过记dn=
,进而计算可得结论;(2)通过记dn= ![]() 可知dn=327n﹣1 , 进而利用等比数列的求和公式计算即得结论.
可知dn=327n﹣1 , 进而利用等比数列的求和公式计算即得结论.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系 .
.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源: 题型:
【题目】一个酒杯的轴截面是一条抛物线的一部分,它的方程是x2=2y,y∈[0,10],在杯内放入一个清洁球,要求清洁球能擦净酒杯的最底部(如图),则清洁球的最大半径为 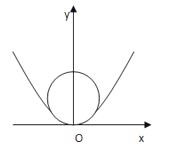
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的首项为a1=1,且 ![]() ,(n∈N*).
,(n∈N*).
(1)求a2 , a3的值,并证明:a2n﹣1<a2n+1<2;
(2)令bn=|a2n﹣1﹣2|,Sn=b1+b2+…+bn . 证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在R上的函数f(x),如果存在实数a,使得f(a+x)f(a﹣x)=1对任意实数x∈R恒成立,则称f(x)为关于a的“倒函数”.已知定义在R上的函数f(x)是关于0和1的“倒函数”,且当x∈[0,1]时,f(x)的取值范围为[1,2],则当x∈[1,2]时,f(x)的取值范围为 , 当x∈[﹣2016,2016]时,f(x)的取值范围为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设{an}是等比数列,下列结论中正确的是( )
A.若a1+a2>0,则a2+a3>0
B.若a1+a3<0,则a1+a2<0
C.若0<a1<a2 , 则2a2<a1+a3
D.若a1<0,则(a2﹣a1)(a2﹣a3)>0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,关于x的方程f2(x)﹣2af(x)+a﹣1=0(a∈R)有四个相异的实数根,则a的取值范围是( )
,关于x的方程f2(x)﹣2af(x)+a﹣1=0(a∈R)有四个相异的实数根,则a的取值范围是( )
A.(﹣1, ![]() )
)
B.(1,+∞)
C.( ![]() ,2)
,2)
D.( ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+ax+1,g(x)=ex(其中e为自然对数的底数). (Ⅰ)若a=1,求函数y=f(x)g(x)在区间[﹣2,0]上的最大值;
(Ⅱ)若a=﹣1,关于x的方程f(x)=kg(x)有且仅有一个根,求实数k的取值范围;
(Ⅲ)若对任意的x1 , x2∈[0,2],x1≠x2 , 不等式|f(x1)﹣f(x2)|<|g(x1)﹣g(x2)|均成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,平面PAB⊥平面ABC,AP⊥BP,AC⊥BC,∠PAB=60°,∠ABC=45°,D是AB中点,E,F分别为PD,PC的中点.
(Ⅰ)求证:AE⊥平面PCD;
(Ⅱ)求二面角B﹣PA﹣C的余弦值;
(Ⅲ)在棱PB上是否存在点M,使得CM∥平面AEF?若存在,求 ![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com