
某次考试中,从甲、乙两个班各随机抽取10名学生的成绩进行统计分析,学生成绩的茎叶图如图所示,成绩不小于90分为及格.
(1)从每班抽取的学生中各随机抽取一人,求至少有一人及格的概率
(2)从甲班10人中随机抽取一人,乙班10人中随机抽取两人,三人中及格人数记为X,求X的分布列和期望.

(1)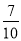 ;
;
(2)
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
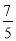 .
.
【解析】
试题分析:
解题思路:(1)先由茎叶图得出有关数据,利用对立事件求概率;(2)列出随机变量的所有可能求值,求出各自的概率,列表得出分布列,进而求出期望值.
规律总结:以图表给出的统计题目一般难度不大,主要考查频率直方图、茎叶图、频率分布表给出;对于“至少”、“至多”,可以考虑事件的对立事件..
试题解析:(1)由茎叶图可知:甲班有4人及格,乙班有5人及格,
设事件“从每班10名同学中各抽取一人,至少有一人及格”为事件A.
则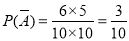 ,
,
所以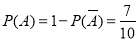 .
.
(2)由题意可知X的所有可能取值为0,1,2,3.
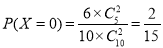 ;
;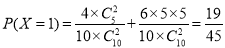 ;
;
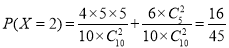 ;
;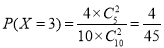 .
.
所以X的分布列为
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
因此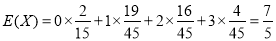 .
.
考点:1.茎叶图;2.随机事件的概率;3.离散型随机变量的分布列与期望.


科目:高中数学 来源:2015届河北省邯郸市高三上学期摸底考试文科数学试卷(解析版) 题型:选择题
4张卡片上分别写有数字1,2,3,4,从这4张卡片中随机抽取2张,则取出的2张卡片上的数学之和为偶数的概率是( )
A.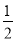 B.
B.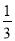 C.
C.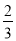 D.
D.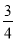
查看答案和解析>>
科目:高中数学 来源:2015届河北省石家庄市高二下学期期末考试理科数学试卷(解析版) 题型:解答题
已知圆C1的参数方程为 (φw为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C2的极坐标方程为ρ=4sin(θ+
(φw为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C2的极坐标方程为ρ=4sin(θ+ ).
).
(1)将圆C1的参数方程化为普通方程,将圆C2的极坐标方程化为直角坐标系方程;
(2)圆C1,C2是否相交?请说明理由.
查看答案和解析>>
科目:高中数学 来源:2015届河北省石家庄市高二下学期期末考试理科数学试卷(解析版) 题型:填空题
若(x+m)9=a0+a1(x+1)+a2(x+1)2+…+a9(x+1)9,且a0﹣a1+a2﹣a3+…+a8﹣a9=39,则实数m的值为 .
查看答案和解析>>
科目:高中数学 来源:2015届河北省石家庄市高二下学期期末考试理科数学试卷(解析版) 题型:选择题
已知盒中装有3个红球、2个白球、5个黑球,它们大小形状完全相同,现需一个红球,甲每次从中任取一个不放回,在他第一次拿到白球的条件下,第二次拿到红球的概率( ).
A.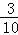 B.
B. C.
C.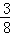 D.
D.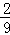
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com