练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若点p是抛物线y＝x2上任意一点，则点p到直线y＝x－2的最小距离为________．

    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：学习周报　数学　人教课标高二版(A选修1－1)　2009－2010学年　第26期　总第182期 人教课标版(A选修1－1) 题型：013

    点P在直线l：y＝x－1上，若存在过P的直线交抛物线y＝x2于A，B两点，且|PA|＝|AB|，则称点P为“δ点”，那么下列结论中正确的是

    [　　]
    A．

    直线l上的所有点都是“δ点”

    B．

    直线l上仅有有限个点是“δ点”

    C．

    直线l上的所有点都不是“δ点”

    D．

    直线l上有无穷多个点(不是所有的点)是“δ点”

    查看答案和解析>>

    科目：高中数学 来源：湖北省黄冈中学、黄石二中2011－2012学年高二下学期期中联考数学文科试题 题型：044

    如图，P是抛物线C：x2＝2y上一点，F为抛物线的焦点，直线l过点P且与抛物线交于另一点Q，已知P(x1，y1)，Q(x2，y2)．

    (1)若l经过点F，求弦长|PQ|的最小值；

    (2)设直线l：y＝kx＋b(k≠0，b≠0)与x轴交于点S，与y轴交于点T．

    ①求证：

    ②求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：上海市徐汇区2010届高三第二次模拟考试数学理科试题 题型：044

    设P(a，b)(a·b≠0)、R(a，2)为坐标平面xoy上的点，直线OR(O为坐标原点)与抛物线y2＝x交于点Q(异于O)．

    (1)若对任意ab≠0，点Q在抛物线y＝mx2＋1(m≠0)上，试问当m为何值时，点P在某一圆上，并求出该圆方程M；

    (2)若点P(a，b)(ab≠0)在椭圆x2＋4y2＝1上，试问：点Q能否在某一双曲线上，若能，求出该双曲线方程，若不能，说明理由；

    (3)对(1)中点P所在圆方程M，设A、B是圆M上两点，且满足|OA|·|OB|＝1，试问：是否存在一个定圆S，使直线AB恒与圆S相切．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

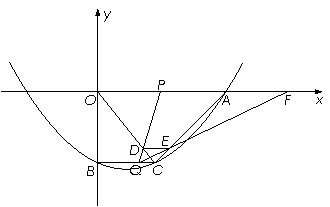
    如图，在平面直角坐标系xoy中，抛物线y＝x 2－x－10与x轴的交点为A，与y轴的交点为点B，过点B作x轴的平行线BC，交抛物线于点C，连结AC．现有两动点P，Q分别从O，C两点同时出发，点P以每秒4个单位的速度沿OA向终点A移动，点Q以每秒1个单位的速度沿CB向点B移动，点P停止运动时，点Q也同时停止运动．线段OC，PQ相交于点D，过点D作DE∥OA，交CA于点E，射线QE交x轴于点F．设动点P，Q移动的时间为t(单位：秒)

    （1）求A，B，C三点的坐标和抛物线的顶点坐标；

    （2）当t为何值时，四边形PQCA为平行四边形？请写出计算过程；

    （3）当t∈（0，）时，△PQF的面积是否总为定值？若是，求出此定值；若不是，请说明理由；

    （4）当t为何值时，△PQF为等腰三角形？请写出解答过程．

     


    查看答案和解析>>

    同步练习册答案