
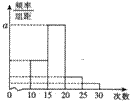
 对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数根据此教据作出了频数与频率的统计表和频率分布直方图:
对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数根据此教据作出了频数与频率的统计表和频率分布直方图:| 分组 | 频数 | 频率 | 奖品价值(元) |
| [10,25) | 5 | 0.25 | 20 |
| [15,20) | 12 | n | 40 |
| [20,25) | m | p | 60 |
| [25,30) | 1 | 0.05 | 80 |
| 合计 | M | 1 |
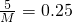 ,
, ,
,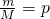 ,
,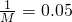 ,
,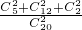 =
=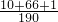 =
=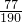 ,
, =
=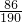 ,
,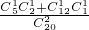 =
=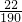 ,
,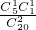 =
=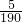 ,
,| X | 0 | 20 | 40 | 60 |
| P | 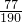 | 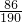 | 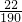 | 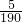 |
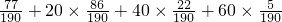 =
=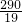 .
.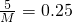 ,
, ,
,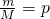 ,
,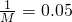 ,5+12+m+1=M,由此能求出表中M,p及图中a的值.
,5+12+m+1=M,由此能求出表中M,p及图中a的值.

科目:高中数学 来源: 题型:解答题
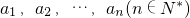 ,任意选取一个实数c,变换T(c)将数列a1,a2,…,an变换为数列|a1-c|,|a2-c|,…,|an-c|,再将得到的数列继续实施这样的变换,这样的变换可以连续进行多次,并且每次所选择的实数c可以不相同,第k(k∈N*)次变换记为Tk(ck),其中ck为第k次变换时选择的实数.如果通过k次变换后,数列中的各项均为0,则称T1(c1),T2(c2),…,Tk(ck)为“k次归零变换”.
,任意选取一个实数c,变换T(c)将数列a1,a2,…,an变换为数列|a1-c|,|a2-c|,…,|an-c|,再将得到的数列继续实施这样的变换,这样的变换可以连续进行多次,并且每次所选择的实数c可以不相同,第k(k∈N*)次变换记为Tk(ck),其中ck为第k次变换时选择的实数.如果通过k次变换后,数列中的各项均为0,则称T1(c1),T2(c2),…,Tk(ck)为“k次归零变换”.查看答案和解析>>
科目:高中数学 来源: 题型:单选题
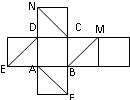 如图是正方体的平面展开图,在这个正方体中;
如图是正方体的平面展开图,在这个正方体中;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com