
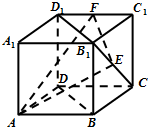
 如图,边长为1的正方体ABCD-A1B1C1D1中,E,F分别是B1C,D1C1的中点,则△AEF在面BB1D1D上的射影的面积为
如图,边长为1的正方体ABCD-A1B1C1D1中,E,F分别是B1C,D1C1的中点,则△AEF在面BB1D1D上的射影的面积为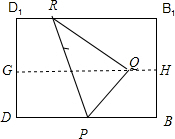
| ||
| 4 |
3
| ||
| 4 |
| ||
| 2 |
| 2 |
| 1 |
| 2 |
| ||
| 4 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 4 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 4 |
3
| ||
| 4 |
3
| ||
| 16 |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| A、画工序流程图类似于算法的流程图,自顶向下逐步细化 |
| B、工序流程图中的流程线表示相邻工序之间的接续关系 |
| C、在工序流程图中可以出现循环回路 |
| D、结构图中基本要素之间一般为概念的从属关系或逻辑上的先后关系 |
查看答案和解析>>
科目:高中数学 来源: 题型:
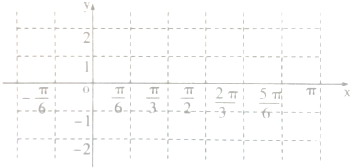
| π |
| 6 |
| π |
| 4 |
| a |
| b |
| 2 |
| 3 |
| A、0 | B、1 | C、2 | D、3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| 3 |
| n |
| m |
| n |
| π |
| 12 |
| 11 |
| 12 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市新都区高三诊断测试理科数学试卷(解析版) 题型:解答题
已知函数f(x)=lnx+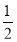 ax2-(a+1)x(a∈R).
ax2-(a+1)x(a∈R).
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)当a>0时,若f(x)在区间[1,e]上的最小值为-2,求实数a的值;
(3)若对?x1,x2∈(0,+∞),x1<x2,且f(x1)+x1<f(x2)+x2恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市新都区高三诊断测试理科数学试卷(解析版) 题型:填空题
函数f(x)=10x+x-7与g(x)=lgx+x-7的零点分别为1和x2,则x1+x2=_______
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市新都区高三诊断测试文科数学试卷(解析版) 题型:解答题
如图,多边形ABCDE中,∠ABC=90°,AD∥BC,△ADE是正三角形,AD=2,AB=BC=1,沿直线AD将△ADE折起至△ADP的位置,连接PB,BC,构成四棱锥P-ABCD,使得∠PAB=90°.点O为线段AD的中点,连接PO.
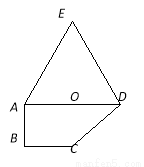

(1)求证:PO⊥平面ABCD;
(2)求异面直线CD与PA所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三10月考文科数学试卷(解析版) 题型:解答题
已知{an}是等差数列,其前n项的和为Sn, {bn}是等比数列,且a1=b1=2,a4+b4=21,S4+b4=30.(1)求数列{an}和{bn}的通项公式;
(2)记cn=anbn,n∈N*,求数列{cn}的前n项和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com