
如图,多边形ABCDE中,∠ABC=90°,AD∥BC,△ADE是正三角形,AD=2,AB=BC=1,沿直线AD将△ADE折起至△ADP的位置,连接PB,BC,构成四棱锥P-ABCD,使得∠PAB=90°.点O为线段AD的中点,连接PO.

(1)求证:PO⊥平面ABCD;
(2)求异面直线CD与PA所成角的余弦值.
(1)见解析;(2)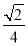
【解析】试题分析:(1)利用线线垂直证明线线垂直,注意“相交直线”这一条件的使用;(2)通过平行线,将异面直线转化为相交直线,再构造三角形,通过余弦定理可求得其余弦值.
试题解析: (1)证明:∵∠ABC=90°,AD∥BC,

(注:证到BA⊥面PAD、PO⊥面ABCD各给3分.)
(2) 取PD中点F,连接BO、OF、BF.
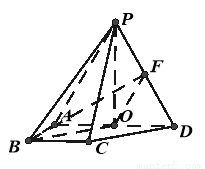
由平几知识可得:OF∥PA,BO∥CD, 1分
∠BOF为所求异面直线PA与CD所成的角或补角. 1分
可求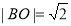 ,|OF|=1,|BF|=2 . 1分
,|OF|=1,|BF|=2 . 1分
在△BOF中,由余弦定理可得: . 2分
. 2分
所求异面直线PA与CD所成角的余弦值为: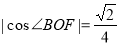 . 1分
. 1分
(注:考生用其它方法求得答案,不扣分.解答步骤参考本答案给分.)
考点:空间线面关系,异面直线所成角


科目:高中数学 来源: 题型:
| A、若m∥n,n?α,则m∥α |
| B、若α⊥β,α∩β=m,n⊥m,则n⊥α |
| C、若l⊥n,m⊥n,则l∥m |
| D、若l⊥α,m⊥β,且l⊥m,则α⊥β |
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市新都区高三诊断测试理科数学试卷(解析版) 题型:选择题
函数f1(x)=x3,f2(x)= ,f3(x)=
,f3(x)= ,f4(x)=
,f4(x)=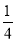 |sin(2πx)|,等差数列{an}中,a1=0,a2015=1,bn=|fk(an+1)-fk(an)|(k=1,2,3,4),用Pk表示数列{bn}的前2014项的和,则( )
|sin(2πx)|,等差数列{an}中,a1=0,a2015=1,bn=|fk(an+1)-fk(an)|(k=1,2,3,4),用Pk表示数列{bn}的前2014项的和,则( )
A.P4<1=P1=P2<P3=2 B.P4<1=P1=P2<P3<2
C.P4=1=P1=P2<P3=2 D.P4<1=P1<P2<P3=2
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市新都区高三诊断测试文科数学试卷(解析版) 题型:填空题
△ABC中,角A,B,C的对边分别为a,b,c,已知b=8,c=6,a=4,D为边BC的中点,则|AD|=___________.
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市新都区高三诊断测试文科数学试卷(解析版) 题型:选择题
在△ABC中,D,E,F分别是BC,CA,AB的中点,点M是△ABC的重心,则 等于( )
等于( )
A. B.4
B.4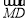 C.4
C.4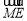 D.4
D.4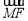
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三10月考理科数学试卷(解析版) 题型:选择题
已知函数f(x)=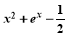 (x<0)与g(x)=
(x<0)与g(x)=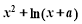 的图象在存在关于y轴对称点,则a的取值范围是( )
的图象在存在关于y轴对称点,则a的取值范围是( )
A、 B、
B、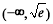 C、
C、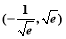 D、
D、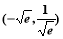
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com