
已知椭圆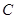 方程为
方程为 ,左、右焦点分别是
,左、右焦点分别是 ,若椭圆
,若椭圆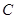 上的点
上的点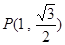 到
到 的距离和等于
的距离和等于 .
.
(Ⅰ)写出椭圆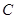 的方程和焦点坐标;
的方程和焦点坐标;
(Ⅱ)设点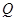 是椭圆
是椭圆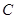 的动点,求线段
的动点,求线段 中点
中点 的轨迹方程;
的轨迹方程;
(Ⅲ)直线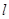 过定点
过定点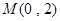 ,且与椭圆
,且与椭圆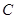 交于不同的两点
交于不同的两点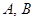 ,若
,若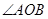 为锐角(
为锐角(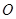 为坐标原点),求直线
为坐标原点),求直线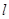 的斜率
的斜率 的取值范围.
的取值范围.
(Ⅰ)椭圆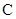 的方程
的方程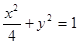 ,焦点
,焦点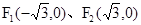
(Ⅱ)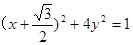 (Ⅲ)
(Ⅲ)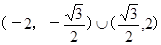
【解析】
试题分析:(Ⅰ)由题意得: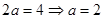 ,
,
又点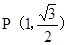 椭圆
椭圆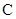 上,∴
上,∴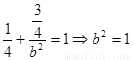
∴ 椭圆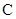 的方程
的方程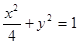 ,焦点
,焦点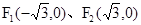 . ……5分
. ……5分
(Ⅱ)设椭圆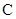 上的动点
上的动点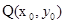 ,线段
,线段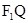 中点
中点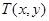 ,
,
由题意得: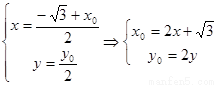 ,
,
代入椭圆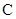 的方程得,
的方程得, ,
,
即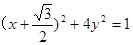 为线段
为线段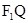 中点
中点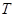 的轨迹方程. ……9分
的轨迹方程. ……9分
(Ⅲ)由题意得直线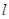 的斜率存在且不为
的斜率存在且不为 ,
,
设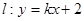 代入
代入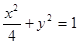 整理,
整理,
得 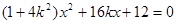 ,
,
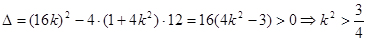 ①
①
设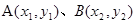 ,∴
,∴ 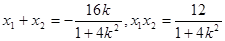
∵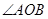 为锐角
为锐角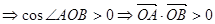 ,即
,即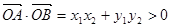 ,
,
又 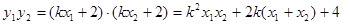 .
.
∴ 
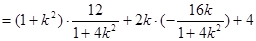
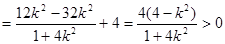 , ∴
, ∴ 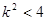 . ②
. ②
由①、②得 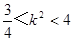 ,∴
,∴ 的取值范围是
的取值范围是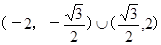 . ……14分
. ……14分
考点:本小题注意考查椭圆标准方程的求解,直线与椭圆的位置关系等.
点评:圆锥曲线的综合问题一般离不开直线方程和圆锥曲线方程联立方程组,运算量较大,注意到联立得到直线方程后,不要忘记验证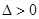 .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| x2 |
| 2 |
| EG |
| F2E |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省成都市高新区高三2月月考理科数学试卷(解析版 题型:填空题
已知椭圆方程为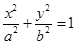 (
(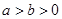 ),F
),F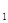 (-c,0)和F
(-c,0)和F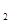 (c,0)分别是椭圆的左 右焦点.
(c,0)分别是椭圆的左 右焦点.
①若P是椭圆上的动点,延长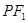 到M,使
到M,使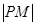 =
=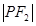 ,则M的轨迹是圆;
,则M的轨迹是圆;
②若P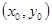 是椭圆上的动点,则
是椭圆上的动点,则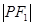
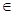
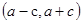 ;
;
③以焦点半径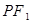 为直径的圆必与以长轴为直径的圆内切;
为直径的圆必与以长轴为直径的圆内切;
④若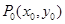 在椭圆
在椭圆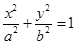 上,则过
上,则过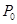 的椭圆的切线方程是
的椭圆的切线方程是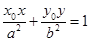 ;
;
⑤点P为椭圆上任意一点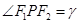 ,则椭圆的焦点角形的面积为
,则椭圆的焦点角形的面积为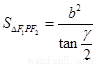 .
.
以上说法中,正确的有
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2012-2013学年上海市闵行区七宝中学高三(下)摸底数学试卷(解析版) 题型:解答题
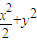 =1,它的左、右焦点分别为F1、F2.点P(x,y)为第一象限内的点.直线PF1和PF2与椭圆的交点分别为A、B和C、D,O为坐标原点.
=1,它的左、右焦点分别为F1、F2.点P(x,y)为第一象限内的点.直线PF1和PF2与椭圆的交点分别为A、B和C、D,O为坐标原点.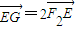 ,求p的最大值.
,求p的最大值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com