
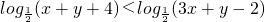 ,若x-y<λ恒成立,则λ的取值范围是
,若x-y<λ恒成立,则λ的取值范围是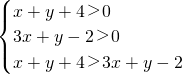 ,画出满足约束条件的可行域,再用角点法,求出目标函数z=x-y的范围,再根据最值给出λ的最大值.
,画出满足约束条件的可行域,再用角点法,求出目标函数z=x-y的范围,再根据最值给出λ的最大值.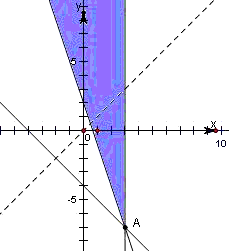 解:由题意得
解:由题意得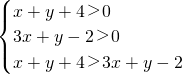 ,即
,即 .
. 表示的可行域如下图示:
表示的可行域如下图示:

科目:高中数学 来源:0110 月考题 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省无锡市江阴市成化高中高三摸底数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com