
【题目】某学校的平面示意图为如下图五边形区域ABCDE,其中三角形区域ABE为生活区,四边形区域BCDE为教学区,AB,BC,CD,DE,EA,BE为学校的主要道路(不考虑宽度). ![]() ,
, ![]() .
. 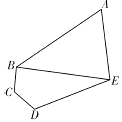
(1)求道路BE的长度;
(2)求生活区△ABE面积的最大值.
科目:高中数学 来源: 题型:
【题目】若实数x,y满足的约束条件  ,将一颗骰子投掷两次得到的点数分别为a,b,则函数z=2ax+by在点(2,﹣1)处取得最大值的概率为( )
,将一颗骰子投掷两次得到的点数分别为a,b,则函数z=2ax+by在点(2,﹣1)处取得最大值的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2lnx+ax﹣ ![]() (a∈R)在x=2处的切线经过点(﹣4,ln2)
(a∈R)在x=2处的切线经过点(﹣4,ln2)
(1)讨论函数f(x)的单调性;
(2)若不等式 ![]() >mx﹣1恒成立,求实数m的取值范围.
>mx﹣1恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了缓解城市交通压力,大力发展公共交通,提倡多坐公交少开车,为了调查市民乘公交车的候车情况,交通主管部门从在某站台等车的![]() 名候车乘客中随机抽取
名候车乘客中随机抽取![]() 人,按照他们的候车时间(单位:分钟)作为样本分成
人,按照他们的候车时间(单位:分钟)作为样本分成![]() 组,如下表所示:
组,如下表所示:
组别 | 一 | 二 | 三 | 四 | 五 | 六 |
候车时间 |
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
(1)估计这![]() 名乘客中候车时间少于
名乘客中候车时间少于![]() 分钟的人数;
分钟的人数;
(2)若从上表第四、五组的![]() 人中随机抽取
人中随机抽取![]() 人做进一步的问卷调查,求抽到的
人做进一步的问卷调查,求抽到的![]() 人恰好来自不同组的概率.
人恰好来自不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应“精确扶贫”号召,某企业计划每年用不超过100万元的资金购买单价分别为1500元/箱和3000元/箱的A、B两种药品捐献给贫困地区某医院,其中A药品至少100箱,B药品箱数不少于A药品箱数.则该企业捐献给医院的两种药品总箱数最多可为( )
A.200
B.350
C.400
D.500
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为 ![]() (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为2ρ2﹣ρ2cos2θ=12.若曲线C的左焦点F在直线l上,且直线l与曲线C交于A,B两点.
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为2ρ2﹣ρ2cos2θ=12.若曲线C的左焦点F在直线l上,且直线l与曲线C交于A,B两点.
(1)求m的值并写出曲线C的直角坐标方程;
(2)求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为a的正方体ABCD﹣A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E,F为CD上任意两点,且EF的长为定值,则下面的四个值中不为定值的是( ) 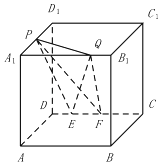
A.点Q到平面PEF的距离
B.直线PE与平面QEF所成的角
C.三棱锥P﹣QEF的体积
D.二面角P﹣EF﹣Q的大小
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把半椭圆![]() (x≥0)与圆弧(x﹣c)2+y2=a2(x<0)合成的曲线称作“曲圆”,其中F(c,0)为半椭圆的右焦点.如图,A1,A2,B1,B2分别是“曲圆”与x轴、y轴的交点,已知∠B1FB2=
(x≥0)与圆弧(x﹣c)2+y2=a2(x<0)合成的曲线称作“曲圆”,其中F(c,0)为半椭圆的右焦点.如图,A1,A2,B1,B2分别是“曲圆”与x轴、y轴的交点,已知∠B1FB2=![]() ,扇形FB1A1B2的面积为
,扇形FB1A1B2的面积为![]() .
.
(1)求a,c的值;
(2)过点F且倾斜角为θ的直线交“曲圆”于P,Q两点,试将△A1PQ的周长L表示为θ的函数;
(3)在(2)的条件下,当△A1PQ的周长L取得最大值时,试探究△A1PQ的面积是否为定值?若是,请求出该定值;若不是,请求出面积的取值范围.
- 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com