Question

（文）设x，y满足约束条件：

0≤x≤1 0≤y≤1 y-x≥ 1 2

，则z=4-2x+y的最大值是（　　）

A．3

B．4

C．5

D．6

Answer 1

分析：先根据约束条件画出可行域，设z=4-2x+y，再利用z的几何意义求最值，只需求出直线z=4-2x+y过可行域内的点A时，从而得到z最大值即可．

解答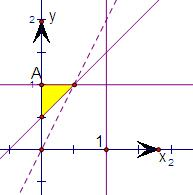：解：先根据约束条件画出可行域，易知可行域为一个三角形，
其3个顶点分别为（0，

1

2

），（0，1），（

1

2

，1），
设z=4-2x+y，将最大值转化为y轴上的截距，
当直线z=4-2x+y经过点A（0，1）时，z最大为5，
故选C．．

点评：本小题主要考查线性规划问题，以及简单的转化思想和数形结合的思想，属中档题．目标函数有唯一最优解是我们最常见的问题，这类问题一般要分三步：画出可行域、求出关键点、定出最优解．