Question

（07年浙江卷文）(14分)在如图所示的几何体中，EA⊥平面ABC，DB⊥平面ABC，AC⊥BC，且AC=BC=BD=2AE，M是AB的中点．(I)求证：CM ⊥EM： (Ⅱ)求DE与平面EMC所成角的正切值．

Answer 1

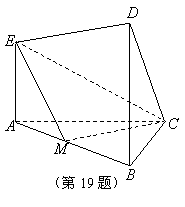
解析：(I)证明：因为AC=BC，M是AB的中点，所以CM⊥AB．

    又EA ⊥平面ABC， ∴ EA ⊥CM，且

   ∴ ，所以CM⊥EM．

(Ⅱ) 连接MD,设AE=a,则BD=BC=AC=2a,

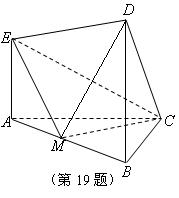
在直角梯形EABD中，AB=，M是AB中点，所以DE=3a,，MD=,因此.因为CM⊥平面EMD，所以CM⊥DM，因此DM⊥平面EMC

故是直线DE与平面EMC所成角。

在中，MD=，，

∴

【高考考点】空间线面关系、直线与平面所成角的求法

【易错点】：找不出或找错直线与平面所成角。

【备考提示】：本题主要考查空间线面关系、直线与平面所成角的求法等基础知识，同时考查空间想象能力和推理能力． 对于线面垂直问题，最常用的方法是通过线面垂直去证明，而求直线与平面所成角，首先要作出所求的角，再求之。同时，利用空间向量也是解决此类问题的一个重要的方法，大家可以尝试一下。