Question

已知函数{a_n}满足a₁=1，a_n+1-a_n=2n+1
（I）求{a_n}的通项公式；
（II）求-a₁+a₂-a₃+…+（-1）ⁿa_n．

Answer 1

【答案】分析：（I）由已知，数列后项与前项之差成等差数列，可用当n≥2 时  a_n=a₁+（a₂-a₁）+（a₃-a₂）+…+（a_n-a _n-1）求解．
（II）观察式子特点，利用a²-b²=（a+b）（a-b）将项进行降次，转化成有特殊性质的数列求和．
解答：解：（I）当n≥2 时  a_n=a₁+（a₂-a₁）+（a₃-a₂）+…+（a_n-a _n-1）=1+3+5+…+（2n-1）=n²    
且对于n=也成立，∴a_n=n²  
（II）记Sn=-a₁+a₂-a₃+…+（-1）ⁿa_n．
当为偶数时Sn=（-1²+2²）+（-3²+4²）++…[（n-1）²-n²]
=（1+2）+（3+4）+…[（n-1）+（n）]
=  
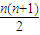
当为奇数时
Sn=-1²+（2²-3²）+（4²-5²）+…[（n-1）²-n²]
=-1-（2+3）-（4+5）-…-[（n-1）+n]
=-
综上，Sn=（-1）^n•
点评：本题考查累和法，分组法数列求和，以及转化的思想方法．要注意n的奇偶性对分组的影响．