
【题目】哈尔滨市第三中学校响应教育部门疫情期间“停课不停学”的号召,实施网络授课,为检验学生上网课的效果,高三学年进行了一次网络模拟考试.全学年共![]() 人,现从中抽取了
人,现从中抽取了![]() 人的数学成绩,绘制成频率分布直方图(如下图所示).已知这
人的数学成绩,绘制成频率分布直方图(如下图所示).已知这![]() 人中
人中![]() 分数段的人数比
分数段的人数比![]() 分数段的人数多
分数段的人数多![]() 人.
人.
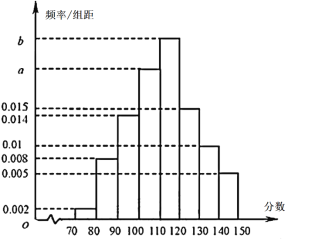
(1)根据频率分布直方图,求![]() 、
、![]() 的值,并估计抽取的
的值,并估计抽取的![]() 名同学数学成绩的中位数;
名同学数学成绩的中位数;
(2)若学年打算给数学成绩不低于![]() 分的同学颁发“网络课堂学习优秀奖”,将这
分的同学颁发“网络课堂学习优秀奖”,将这![]() 名同学数学成绩的样本频率视为概率.
名同学数学成绩的样本频率视为概率.
(i)估计全学年的获奖人数;
(ii)若从全学年随机选取![]() 人,求所选
人,求所选![]() 人中至少有
人中至少有![]() 人获奖的概率.
人获奖的概率.
【答案】(1)![]() ,
,![]() ,中位数为
,中位数为![]() ;(2)(i)
;(2)(i)![]() 人;(ii)
人;(ii)![]() .
.
【解析】
(1)根据题意得出关于![]() 、
、![]() 的方程组,可解得
的方程组,可解得![]() 、
、![]() 的值,再由中位数左边的矩形面积之和为
的值,再由中位数左边的矩形面积之和为![]() 可求得中位数的值;
可求得中位数的值;
(2)(i)计算得出数学成绩不低于![]() 分的同学的频率,乘以
分的同学的频率,乘以![]() 可得出全学年的获奖人数;
可得出全学年的获奖人数;
(ii)设所选![]() 人中获奖人数为
人中获奖人数为![]() ,则
,则![]() ,然后利用独立重复试验的概率公式可求得所求事件的概率.
,然后利用独立重复试验的概率公式可求得所求事件的概率.
(1)依题意![]() ,得
,得![]() ,
,
在所抽取的![]() 人中
人中![]() 分数段的人数比
分数段的人数比![]() 分数段的人数多
分数段的人数多![]() 人,
人,
则![]() ,得
,得![]() ,
,
即![]() ,解得
,解得![]() .
.
设中位数为![]() ,前
,前![]() 个矩形的面积之和为
个矩形的面积之和为![]() ,
,
前![]() 个矩形的面积之和为
个矩形的面积之和为![]() ,
,![]() ,
,
由题意可得![]() ,解得
,解得![]() ;
;
(2)(i)数学成绩不低于![]() 分的同学的频率为
分的同学的频率为![]() ,
,
所以估计全学年获奖人数为![]() 人;
人;
(ii)设所选![]() 人中获奖人数为
人中获奖人数为![]() ,则
,则![]() ,
,
则![]() ,
,
所以所选![]() 人中至少有
人中至少有![]() 人获奖的概率为
人获奖的概率为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知四边形![]() 是梯形(如图1),
是梯形(如图1),![]() ,
,![]() ,
,![]() ,
,![]() ,E为
,E为![]() 的中点,以
的中点,以![]() 为折痕把
为折痕把![]() 折起,使点D到达点P的位置(如图2),且
折起,使点D到达点P的位置(如图2),且![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求点C到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“新冠肺炎”疫情的控制需要根据大数据进行分析,并有针对性的采取措施.下图是甲、乙两个省份从2月7日到2月13日一周内的新增“新冠肺炎”确诊人数的折线图.根据图中甲、乙两省的数字特征进行比对,下列说法错误的是( )
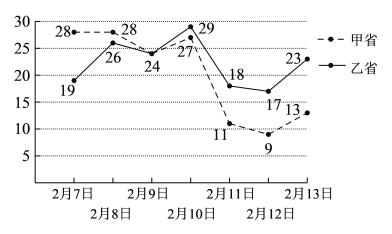
A.2月7日到2月13日甲省的平均新增“新冠肺炎”确诊人数低于乙省
B.2月7日到2月13日甲省的单日新增“新冠肺炎”确诊人数最大值小于乙省
C.2月7日到2月13日乙省相对甲省的新增“新冠甲省肺炎”确诊人数的波动大
D.后四日(2月10日至13日)乙省每日新增“新冠肺炎”确诊人数均比甲省多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题,其中正确命题的个数为( )
①若样本数据![]() ,
,![]() ,…,
,…,![]() 的方差为2,则数据
的方差为2,则数据![]() ,
,![]() ,…,
,…,![]() 的方差为4;
的方差为4;
②回归方程为![]() 时,变量x与y具有负的线性相关关系;
时,变量x与y具有负的线性相关关系;
③随机变量X服从正态分布![]() ,
,![]() ,则
,则![]() ;
;
④甲同学所在的某校高三共有5003人,先剔除3人,再按系统抽样的方法抽取容量为200的一个样本,则甲被抽到的概率为![]() .
.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() :
:![]() 的左、右焦点分别是
的左、右焦点分别是![]() ,
,![]() ,离心率为
,离心率为![]() ,左、右顶点分别为
,左、右顶点分别为![]() ,
,![]() .过
.过![]() 且垂直于
且垂直于![]() 轴的直线被椭圆
轴的直线被椭圆![]() 截得的线段长为1.
截得的线段长为1.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)经过点![]() 的直线与椭圆
的直线与椭圆![]() 相交于不同的两点
相交于不同的两点![]() 、
、![]() (不与点
(不与点![]() 、
、![]() 重合),直线
重合),直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,求证:
,求证:![]() 、
、![]() 、
、![]() 三点共线.
三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我校甲、乙、丙三名语文老师和![]() 、
、![]() 、
、![]() 三名数学老师被派往某县城一中和二中支教,其中有一名语文老师和一名数学老师被派到了一中,其它老师都去二中支教,则甲与
三名数学老师被派往某县城一中和二中支教,其中有一名语文老师和一名数学老师被派到了一中,其它老师都去二中支教,则甲与![]() 被派到同一所学校的概率为( )
被派到同一所学校的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com