
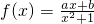 在点M(-1,y0)的切线方程为x+y+3=0.
在点M(-1,y0)的切线方程为x+y+3=0.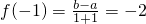 ,化简得b-a=-4①.…(4分)
,化简得b-a=-4①.…(4分)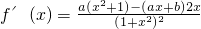 ,则
,则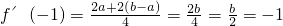 ②.…(6分)
②.…(6分)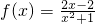 . …(8分)
. …(8分) 在[1,+∞)上恒成立
在[1,+∞)上恒成立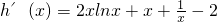
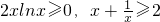 ,即h'(x)≥0.…(12分)
,即h'(x)≥0.…(12分) 在[1,+∞)上恒成立,转化为证明x2lnx+lnx-2x+2≥0在[1,+∞)上恒成立,构造函数,利用导数确定函数的单调性,即可证得结论.
在[1,+∞)上恒成立,转化为证明x2lnx+lnx-2x+2≥0在[1,+∞)上恒成立,构造函数,利用导数确定函数的单调性,即可证得结论.

科目:高中数学 来源:福建省四地六校2012届高三第一次联考数学文科试题 题型:044
已知函数![]() 在点M(-1,y0)的切线方程为x+y+3=0.
在点M(-1,y0)的切线方程为x+y+3=0.
(Ⅰ)求点M的坐标;
(Ⅱ)求函数f(x)的解析式;
(Ⅲ)设g(x)=lnx,求证:g(x)≥f(x)在x∈[1,+∞)上恒成立.
查看答案和解析>>
科目:高中数学 来源:黑龙江省大庆铁人中学2012届高三上学期期中考试数学文科试题 题型:044
已知函数![]() 在点M(-1,y0)的切线方程为x+y+3=0.
在点M(-1,y0)的切线方程为x+y+3=0.
(Ⅰ)求点M的坐标;
(Ⅱ)求函数f(x)的解析式;
(Ⅲ)设g(x)=lnx,求证:g(x)≥f(x)在x∈[1,+∞)上恒成立.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省武汉市部分重点中学高三(上)起点考试数学试卷(文科)(解析版) 题型:解答题
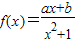 在点M(-1,y)的切线方程为x+y+3=0.
在点M(-1,y)的切线方程为x+y+3=0.查看答案和解析>>
科目:高中数学 来源:2013年山东省临沂市高考数学三模试卷(文科)(解析版) 题型:解答题
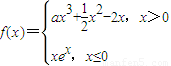 在点A(1,f(1))处的切线l的斜率为零.
在点A(1,f(1))处的切线l的斜率为零.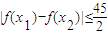 恒成立,这样的m是否存在?若存在,请求出m的取值范围;若不存在,请说明理由.
恒成立,这样的m是否存在?若存在,请求出m的取值范围;若不存在,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com