
【题目】某商场春节期间推出一项优惠活动,活动规则如下:消费额每满300元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置.若指针停在区域Ⅰ返券60元;停在区域Ⅱ返券30元;停在区域Ⅲ不返券.例如:消费600元,可抽奖2次,所获得的返券金额是两次金额之和.
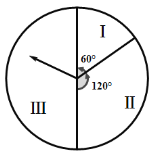
(Ⅰ)若某位顾客消费300元,求返券金额不低于30元的概率;
(Ⅱ)若某位顾客恰好消费600元,并按规则参与了活动,他获得返券的金额记为![]() (元).求随机变量
(元).求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
【答案】(Ⅰ)![]() (Ⅱ)见解析,40
(Ⅱ)见解析,40
【解析】
(Ⅰ)设指针落在区域Ⅰ、Ⅱ、Ⅲ分别记为事件![]() 、
、![]() 、
、![]() ,则
,则![]() ,
,![]() ,
,![]() ,若返券金额不低于30元,则指针落在区域Ⅰ或区域Ⅲ,再根据和事件求概率即可;
,若返券金额不低于30元,则指针落在区域Ⅰ或区域Ⅲ,再根据和事件求概率即可;
(Ⅱ)随机变量![]() 的可能取值为0,30,60,90,120,然后结合独立事件依次求出每个
的可能取值为0,30,60,90,120,然后结合独立事件依次求出每个![]() 的取值所对应的概率即可得到分布列,再求数学期望即可得解.
的取值所对应的概率即可得到分布列,再求数学期望即可得解.
解:(Ⅰ)设指针落在区域Ⅰ、Ⅱ、Ⅲ分别记为事件![]() 、
、![]() 、
、![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
若返券金额不低于30元,则指针落在区域Ⅰ或区域Ⅲ的概率为![]() ,
,
即消费300元的顾客,返券金额不低于30元的概率是![]() .
.
(Ⅱ)由题意得,该顾客可转动转盘2次,随机变量![]() 的可能取值为0,30,60,90,120,
的可能取值为0,30,60,90,120,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
所以,随机变量![]() 的分布列为
的分布列为
| 0 | 30 | 60 | 90 | 120 |
|
|
|
|
|
|
数学期望![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 内,动点
内,动点![]() 到定点
到定点![]() 的距离与
的距离与![]() 到定直线
到定直线![]() 距离之比为
距离之比为![]() .
.
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)设点![]() 是轨迹
是轨迹![]() 上两个动点直线
上两个动点直线![]() 与轨迹
与轨迹![]() 的另一交点分别为
的另一交点分别为![]() 且直线
且直线![]() 的斜率之积等于
的斜率之积等于![]() ,问四边形
,问四边形![]() 的面积
的面积![]() 是否为定值?请说明理由.
是否为定值?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC—A1B1C1中,AA1=AC,A1B⊥AC1,设O为AC1与A1C的交点,点P为BC的中点.求证:
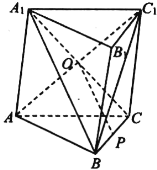
(1)OP∥平面ABB1A1;
(2)平面ACC1⊥平面OCP.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医院体检中心为回馈大众,推出优惠活动:对首次参加体检的人员,按200元/次收费,并注册成为会员,对会员的后续体检给予相应优惠(本次即第一次),标准如下:
体检次序 | 第一次 | 第二次 | 第三次 | 第四次 | 第五次及以上 |
收费比例 | 1 | 0.95 | 0.90 | 0.85 | 0.8 |
该体检中心从所有会员中随机选取了100位对他们在本中心参加体检的次数进行统计,得到数据如下表:
体检次数 | 一次 | 两次 | 三次 | 四次 | 五次及以上 |
频数 | 60 | 20 | 12 | 4 | 4 |
假设该体检中心为顾客体检一次的成本费用为150元,根据所给数据,解答下列问题:
(1)已知某顾客在此体检中心参加了3次体检,求这3次体检,该体检中心的平均利润;
(2)该体检中心要从这100人里至少体检3次的会员中,按体检次数用分层抽样的方法抽出5人,再从这5人中抽取2人发放纪念品,求抽到的2人中恰有1人体检3次的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() (其中
(其中![]() ,
,![]() ,
,![]() )的图象的两条相邻对称轴之间的距离为
)的图象的两条相邻对称轴之间的距离为![]() ,且图象上一个最低点为
,且图象上一个最低点为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)当![]() 时,求函数
时,求函数![]() 的值域;
的值域;
(3)若方程![]() 在
在![]() 上有两个不相等的实数根
上有两个不相等的实数根![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线定位法是通过测定待定点到至少三个已知点的两个距离差所进行的一种无线电定位.通过船(待定点)接收到三个发射台的电磁波的时间差计算出距离差,两个距离差即可形成两条位置双曲线,两者相交便可确定船位.我们来看一种简单的“特殊”状况;如图所示,已知三个发射台分别为![]() ,
,![]() ,
,![]() 且刚好三点共线,已知
且刚好三点共线,已知![]() 海里,
海里,![]() 海里,现以
海里,现以![]() 的中点为原点,
的中点为原点,![]() 所在直线为
所在直线为![]() 轴建系.现根据船
轴建系.现根据船![]() 接收到
接收到![]() 点与
点与![]() 点发出的电磁波的时间差计算出距离差,得知船
点发出的电磁波的时间差计算出距离差,得知船![]() 在双曲线
在双曲线![]() 的左支上,若船
的左支上,若船![]() 上接到
上接到![]() 台发射的电磁波比
台发射的电磁波比![]() 台电磁波早
台电磁波早![]() (已知电磁波在空气中的传播速度约为
(已知电磁波在空气中的传播速度约为![]() ,1海里
,1海里![]() ),则点
),则点![]() 的坐标(单位:海里)为( )
的坐标(单位:海里)为( )
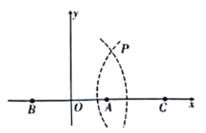
A. B.
B.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区在一次考试后,从全体考生中随机抽取44名,获取他们本次考试的数学成绩(x)和物理成绩(y),绘制成如图散点图:
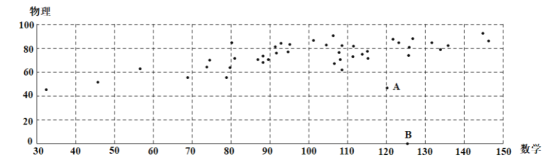
根据散点图可以看出y与x之间有线性相关关系,但图中有两个异常点A,B.经调查得知,A考生由于重感冒导致物理考试发挥失常,B考生因故未能参加物理考试.为了使分析结果更科学准确,剔除这两组数据后,对剩下的数据作处理,得到一些统计的值:![]()
![]()
![]() 其中xi,yi分别表示这42名同学的数学成绩、物理成绩,i=1,2,…,42,y与x的相关系数r=0.82.
其中xi,yi分别表示这42名同学的数学成绩、物理成绩,i=1,2,…,42,y与x的相关系数r=0.82.
(1)若不剔除A,B两名考生的数据,用44组数据作回归分析,设此时y与x的相关系数为r0.试判断r0与r的大小关系,并说明理由;
(2)求y关于x的线性回归方程(系数精确到0.01),并估计如果B考生加了这次物理考试(已知B考生的数学成绩为125分),物理成绩是多少?(精确到个位);
(3)从概率统计规律看,本次考试该地区的物理成绩ξ服从正态分布![]() ,以剔除后的物理成绩作为样本,用样本平均数
,以剔除后的物理成绩作为样本,用样本平均数![]() 作为μ的估计值,用样本方差s2作为σ2的估计值.试求该地区5000名考生中,物理成绩位于区间(62.8,85.2)的人数Z的数学期望.
作为μ的估计值,用样本方差s2作为σ2的估计值.试求该地区5000名考生中,物理成绩位于区间(62.8,85.2)的人数Z的数学期望.
附:①回归方程![]() 中:
中: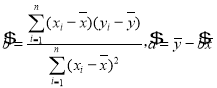
②若![]() ,则
,则![]()
③![]() 11.2
11.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为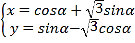 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,取相同长度单位建立极坐标系,直线
轴的正半轴为极轴,取相同长度单位建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 和直线
和直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)直线![]() 与
与![]() 轴交点为
轴交点为![]() ,经过点
,经过点![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() ,
,![]() 两点,证明:
两点,证明:![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com