
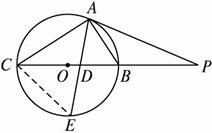
图2-5-16
科目:高中数学 来源: 题型:
 如图,设圆(x-5)2+y2=16的圆心为C,此圆和抛物线y2=px(p>0)有四个交点,若在x轴上方的两个交点为A(x1,
如图,设圆(x-5)2+y2=16的圆心为C,此圆和抛物线y2=px(p>0)有四个交点,若在x轴上方的两个交点为A(x1,| px1 |
| px2 |
| CA |
| CB |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•江苏)A.[选修4-1:几何证明选讲]
(2012•江苏)A.[选修4-1:几何证明选讲]
|
| 2 |
| π |
| 4 |
| π |
| 3 |
| ||
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 5 |
| 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(06年山东卷理)下列四个命题中,真命题的序号有 (写出所有真命题的序号).
①将函数y=![]() 的图象按向量y=(-1,0)平移,得到的图象对应的函数表达式为y=
的图象按向量y=(-1,0)平移,得到的图象对应的函数表达式为y=![]()
②圆x2+y2+4x-2y+1=0与直线y=![]() 相交,所得弦长为2
相交,所得弦长为2
③若sin(![]() +
+![]() )=
)=![]() ,sin(
,sin(![]() -
-![]() )=
)=![]() ,则tan
,则tan![]() cot
cot![]() =5
=5
④如图,已知正方体ABCD- A1B1C1D1,P为底面ABCD内一动点,P到平面AA1D1D的距离与到直线CC1的距离相等,则P点的轨迹是抛物线的一部分.

(16题图)
查看答案和解析>>
科目:高中数学 来源: 题型:
①3 ②4 ③5 ④6 ⑤7
以上结论正确的为_____________.(写出所有正确结论的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
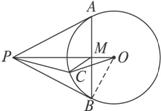
图2-5-16
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com