
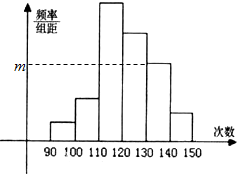
 某校有高二学生1500人,为了了解他们的体能状况,随机抽取了部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形的面积之比为2:4:17:15:9:3,其中第二小组频数为12.
某校有高二学生1500人,为了了解他们的体能状况,随机抽取了部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形的面积之比为2:4:17:15:9:3,其中第二小组频数为12.| (2+4+17+15+9+3)×12 |
| 4 |
| 12 |
| 150 |
| 9 |
| 4 |
| 0.18 |
| 10 |
| 6 |
| 50 |


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 某校高二年级共有学生1000名,其中走读生750名,住宿生250名,现从该年级采用分层抽样的方法从该年级抽取n名学生进行问卷调查.根据问卷取得了这n名同学每天晚上有效学习时间(单位:分钟)的数据,按照以下区间分为八组:
某校高二年级共有学生1000名,其中走读生750名,住宿生250名,现从该年级采用分层抽样的方法从该年级抽取n名学生进行问卷调查.根据问卷取得了这n名同学每天晚上有效学习时间(单位:分钟)的数据,按照以下区间分为八组:| 利用时间充分 | 利用时间不充分 | 总计 | |
| 走读生 | 50 | 25 | 75 |
| 住宿生 | 10 | 15 | 25 |
| 总计 | 60 | 40 | 100 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 利用时间充分 | 利用时间不充分 | 总计 | |
| 走读生 | 50 | 25 | 75 |
| 住宿生 | 10 | 15 | 25 |
| 总计 | 60 | 40 | 100 |
| n(n11n22-n12n21)2 |
| (n22+n21)(n11+n12)(n11+n21)(n12+n21) |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•湖北模拟)某校高二年级共有学生1000名,其中走读生750名,住宿生250名,现从该年级采用分层抽样的方法从该年级抽取n名学生进行问卷调查,根据问卷取得了这n名同学每天晚上有效学习时间(单位:分钟)的数据,按照以下区间分为八组:[0,30),[30,60),[60,90),[90,120),[120,150),[150,180),[180,210),[210.240),得到频率分布直方图如图,已知抽取的学生中每天晚上有效学习时间少于60分钟的人数为5人.
(2012•湖北模拟)某校高二年级共有学生1000名,其中走读生750名,住宿生250名,现从该年级采用分层抽样的方法从该年级抽取n名学生进行问卷调查,根据问卷取得了这n名同学每天晚上有效学习时间(单位:分钟)的数据,按照以下区间分为八组:[0,30),[30,60),[60,90),[90,120),[120,150),[150,180),[180,210),[210.240),得到频率分布直方图如图,已知抽取的学生中每天晚上有效学习时间少于60分钟的人数为5人.| 利用时间充分 | 利用时间不充分 | 合计 | |
| 走读生 | 50 | a | 75 75 |
| 住校生 | b | 15 | 25 25 |
| 合计 | 60 60 |
40 | n |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
P(K2≥k0) |
0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k0 |
0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
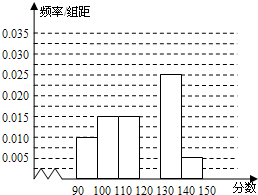 某校从参加高二模拟考试的学生中随机抽取60名学生,将其英语成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如右所示的部分频率分布直方图.观察图形信息,回答下列问题:
某校从参加高二模拟考试的学生中随机抽取60名学生,将其英语成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如右所示的部分频率分布直方图.观察图形信息,回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com