
分析 (Ⅰ)利用零点分段法,将函数解析式化为分段函数的形式,结合二次函数的图象和性质,分析函数的单调性,进而可得函数f(x)在[0,2]上的最小值;
(Ⅱ)要使g(x)有四个不同的零点,则y=ax2+bx-b和y=ax2-bx+b必须分别在[1,+∞)和(-∞,1)上不单调,进而可得答案.
解答 解:(Ⅰ)$f(x)=\left\{{\begin{array}{l}{a{x^2}+x-1(x≥1)}\\{a{x^2}-x+1(x<1)}\end{array}}\right.$
当$\frac{1}{2a}∈({0,1})$,即$\frac{1}{2}<a<4$时,f(x)在$[{0,\frac{1}{2a}}]$上递减,在$[{\frac{1}{2a},2}]$上递增
所以$f{(x)_{min}}=f(\frac{1}{2a})=1-\frac{1}{4a}$
当$\frac{1}{2a}∈[{1,+∞})$,即$0<a≤\frac{1}{2}$时,f(x)在[0,1]上递减,在[1,2]上递增
所以f(x)min=f(1)=a
综上可知,$f{(x)_{min}}=\left\{{\begin{array}{l}{1-\frac{1}{4a}(\frac{1}{2}<a<4)}\\{a(0<a≤\frac{1}{2})}\end{array}}\right.$…(7分)
(Ⅱ)$f(x)=\left\{{\begin{array}{l}{a{x^2}+bx-b(x≥1)}\\{a{x^2}-bx+b(x<1)}\end{array}}\right.$
要使g(x)有四个不同的零点,则y=ax2+bx-b和y=ax2-bx+b必须分别在[1,+∞)和(-∞,1)上不单调
所以$\left\{{\begin{array}{l}{-\frac{b}{2a}>1}\\{\frac{b}{2a}<1}\end{array}}\right.⇒\frac{b}{2a}<-1$,
即$\left\{{\begin{array}{l}{0<a<4}\\{-4<b<-2a}\end{array}}\right.$和$\left\{{\begin{array}{l}{-4<a<0}\\{-2a<b<4}\end{array}}\right.$
由线性规划知识可求得a+b∈(-4,0)∪(0,4)…(15分)
点评 本题考查的知识点是分段函数的应用,二次函数的图象和性质,线性规划,函数零点,难度中档.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 21 | B. | 19 | C. | 9 | D. | -11 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
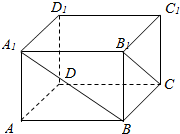 在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3.
在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 128 | B. | 192 | C. | 224 | D. | 256 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com