
【题目】如图甲,E是边长等于2的正方形的边CD的中点,以AE、BE为折痕将△ADE与△BCE折起,使D,C重合(仍记为D),如图乙.
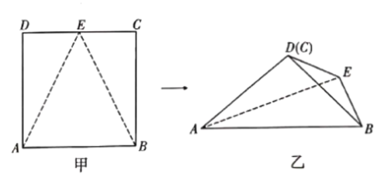
(1)探索:折叠形成的几何体中直线DE的几何性质(写出一条即可,不含DE⊥DA,DE⊥DB,说明理由);
(2)求二面角D-BE-A的余弦值
【答案】(1)几何性质见解析,理由见解析;(2)![]()
【解析】
(1)根据折前折后折痕同侧的位置关系、长度不变,可以证明![]() 平面
平面![]() ,据此结论也可得到
,据此结论也可得到![]() ,或
,或![]() 与平面
与平面![]() 内任一直线都垂直,也可计算直线
内任一直线都垂直,也可计算直线![]() 与平面
与平面![]() 所成角等于
所成角等于![]() ;
;
(2)建立空间直角坐标系,利用向量法可求二面角的余弦值.
(1)性质1:![]() 平面
平面![]() .
.
证明如下:翻折前,![]() ,
,
翻折后仍然![]() ,
,
且![]() ,
,
则![]() 平面
平面![]() .
.
性质2:![]() .
.
证明如下:
与性质1证明方法相同,得到![]() 平面
平面![]() .
.
又因![]() 平面
平面![]() ,则
,则![]() .
.
性质3:![]() 与平面
与平面![]() 内任一直线都垂直.
内任一直线都垂直.
证明如下:
与性质1证明方法相同,得到![]() 平面
平面![]() ,
,
从而![]() 与平面
与平面![]() 内任一直线都垂直.
内任一直线都垂直.
性质4:直线![]() 与平面
与平面![]() 所成角等于
所成角等于![]() .
.
证明如下:
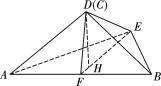
如图,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,
由![]() 得
得![]() ,
,
与性质2证明相同,得![]() ,
,![]()
再因![]() ,则
,则![]() 平面
平面![]() ,进而平面
,进而平面![]() 平面
平面![]() .
.
作![]() 于
于![]() ,则
,则![]() 平面
平面![]() ,
,
即![]() 就是直线
就是直线![]() 与平面
与平面![]() 所成的角.
所成的角.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
(2)与(1)之性质4证明相同,得到![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() 平面
平面![]() 内,则平面
内,则平面![]() 平面
平面![]() .
.
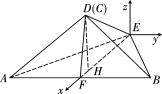
以![]() 为坐标原点、
为坐标原点、![]() 为
为![]() 轴建立如图所示的空间直角坐标系.
轴建立如图所示的空间直角坐标系.
![]() ,
,![]() ,
,![]() ,则平面
,则平面![]() 的一个法向量
的一个法向量![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() .
.
设![]() 是平面
是平面![]() 的法向量,
的法向量,
则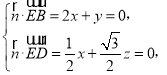
取![]() ,求得一个法向量
,求得一个法向量![]()
记二面角![]() 的大小为
的大小为![]() ,则
,则![]() 与
与![]() 相等或互补,
相等或互补,
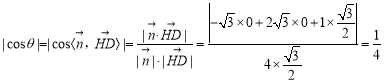 ,
,
因![]() 是锐角,则
是锐角,则![]() .
.


科目:高中数学 来源: 题型:
【题目】过抛物线C:x2=4y的准线上任意一点P作抛物线的切线PA,PB,切点分别为A,B,则A点到准线的距离与B点到准线的距离之和的最小值是( )
A.7B.6C.5D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为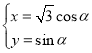 (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 为曲线
为曲线![]() 上位于第一,二象限的两个动点,且
上位于第一,二象限的两个动点,且![]() ,射线
,射线![]() 交曲线
交曲线![]() 分别于
分别于![]() ,求
,求![]() 面积的最小值,并求此时四边形
面积的最小值,并求此时四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,ABCD为菱形,
中,ABCD为菱形,![]() 平面ABCD,连接AC,BD交于点O,
平面ABCD,连接AC,BD交于点O,![]() ,
,![]() ,E是棱PC上的动点,连接DE.
,E是棱PC上的动点,连接DE.
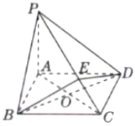
(1)求证:平面![]() 平面
平面![]() ;
;
(2)当![]() 面积的最小值是4时,求此时点E到底面ABCD的距离.
面积的最小值是4时,求此时点E到底面ABCD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直线PQ与⊙O相切于点A,AB是⊙O的弦,∠PAB的平分线AC交⊙O于点C,连结CB,并延长与直线PQ相交于点Q,若AQ=6,AC=5.
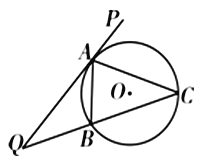
(Ⅰ)求证:QC2﹣QA2=BC![]() QC;
QC;
(Ⅱ)求弦AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】试在①![]() ,②
,②![]() ,③
,③![]() 三个条件中选两个条件补充在下面的横线处,使得
三个条件中选两个条件补充在下面的横线处,使得![]() 面ABCD成立,请说明理由,并在此条件下进一步解答该题:
面ABCD成立,请说明理由,并在此条件下进一步解答该题:
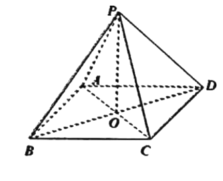
如图,在四棱锥![]() 中,
中,![]() ,底ABCD为菱形,若__________,且
,底ABCD为菱形,若__________,且![]() ,异面直线PB与CD所成的角为
,异面直线PB与CD所成的角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com