练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知函数f（x+1）=x2-2x+1的定义域为[-2，0]，则函数f（x）的最大值为
     
    ．
    考点：二次函数在闭区间上的最值
    专题：函数的性质及应用
    分析：首先求出函数的解析式，然后求二次函数的最值．
    解答： 解：因为f（x+1）=x2-2x+1=（x+1）2-4（x+1）+4，
    所以函数解析式为f（x）=x2-4x+4，
    又因为f（x+1）=x2-2x+1的定义域为[-2，0]，所以x+1∈[-1，1]，
    所以f（x）的定义域为[-1，1]，并且f（x）在[-1，1]上是减函数，
    所以f（x）的最大值为f（-1）=1+4+4=9；
    故答案为：9．
    点评：本题考查了复合函数的定义域求法、解析式的求法以及二次函数解析式最值求法．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知动圆P与圆C1：（x+1）2+y2=
    1
    8
    外切，与圆C2（x-1）2+y2=
    49
    8
    内切．
    （1）求动圆的圆心P的轨迹C的方程；
    （2）设点M（
    1
    4
    ，0），是否存在过点F（1，0）且与x轴不垂直的直线l与轨迹C交于A、B两点，使得
    MA
    +
    MB
    ⊥
    AB
    ？若存在，求出直线l的方程；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    定义运算a?b=
    a，a≤b
    b，a＞b
    ，已知函数f（x）=x?（-x2+2），则f（x）的最大值为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图是某几何体的三视图，其俯视图是半径为2的圆，则该几何体的表面积为
     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

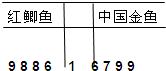    已知某人工养殖观赏鱼池塘中养殖着大量的红鲫鱼与中国金鱼．为了估计池塘中这两种鱼的数量，养殖人员从水库中捕出了红鲫鱼与中国金鱼各1000只，给每只鱼作上不影响其存活的记号，然后放回池塘，经过一定时间，再每次从池塘中随机地捕出1000只鱼，分类记录下其中有记号的鱼的数目，随即将它们放回池塘中．这样的记录作了10次．并将记录获取的数据做成以下的茎叶图，
    （Ⅰ）根据茎叶图计算有记号的红鲫鱼与中国金鱼数目的平均数，并估计池塘中的红鲫鱼与中国金鱼的数量；
    （Ⅱ）假设随机地从池塘逐只有放回地捕出5只鱼中的红鲫鱼的数目为ξ，求ξ的分布列与数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知f（x）=cos（
    2π
    3
    -x）+sin（
    π
    2
    +x）（x∈R）．
    （1）求函数f（x）的最小正周期；
    （2）当x∈[-
    π
    6
    ，
    π
    3
    ]时，求函数f（x）值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知向量
    a
    =（sinθ，-2）与
    b
    =（1，cosθ）互相垂直，其中θ∈（0，
    π
    2
    ），则
    1
    sin2θ
    =（　　）
    A、
    5
    4
    B、
    3
    4
    C、
    4
    5
    D、
    		2
    3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    数列{an}中，已知an=2n-17，该数列中相邻两项积为负数的是（　　）
    A、a6和a7
    B、a7和a8
    C、a8和a9
    D、a9和a10

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    点P（1，2）关于直线x+2y-10=0的对称点坐标为
     
    ．

    查看答案和解析>>

    同步练习册答案