
【题目】下列命题中正确的个数为( )
①“ac<0”是“二次函数y=ax2+bx+c(a,b,c∈R)有两个异号零点”的必要不充分条件;
②”sinθ![]() ”是“θ
”是“θ![]() ”充分不必要条件;
”充分不必要条件;
③“偶函数的图象关于直线x=0成轴对称”的逆否命题;
④“若sinx﹣cosx![]() ,则sinx+cosx
,则sinx+cosx![]() 的逆命题;
的逆命题;
⑤设a,b∈R,则“a>b”是“a|a|>b|b|”的充分条件
A.1B.2C.2D.3
【答案】B
【解析】
对①,根据充分与必要条件的性质判定即可.
对②,判断“![]() ”的充要条件,再分析即可.
”的充要条件,再分析即可.
对③,根据逆否命题与原命题的真假性判定即可.
对④,根据同角三角函数的公式推导判定即可.
对⑤,分析函数![]() 的单调性判定即可.
的单调性判定即可.
对①,当![]() 时,易得二次方程
时,易得二次方程![]() 判别式
判别式![]() ,故
,故![]() 有两根
有两根![]() 且满足
且满足![]() .故“
.故“![]() ”是“二次函数
”是“二次函数![]() 有两个异号零点”的充分条件.
有两个异号零点”的充分条件.
当二次函数![]() 有两个异号零点时可设两根
有两个异号零点时可设两根![]() ,此时
,此时![]() ,故
,故![]() .故“
.故“![]() ”是“二次函数
”是“二次函数![]() 有两个异号零点”的必要条件.
有两个异号零点”的必要条件.
故“![]() ”是“二次函数
”是“二次函数![]() 有两个异号零点”的充要条件.
有两个异号零点”的充要条件.
故①错误.
对②,![]() ,则
,则![]() .故“
.故“![]() ”是“
”是“![]() ”的必要不充分条件.故②错误.
”的必要不充分条件.故②错误.
对③, 偶函数的图象关于直线![]() 成轴对称为真命题,故其逆否命题也为真命题.
成轴对称为真命题,故其逆否命题也为真命题.
故③正确.
对④,原命题的逆命题为“若![]() ,则
,则![]() ”.
”.
当![]() 时,
时, ![]()
![]() .
.
故![]() .
.
故④错误.
对⑤,因为![]() 为奇函数,且在
为奇函数,且在![]() 时为增函数,故
时为增函数,故![]() 为增函数.
为增函数.
故当![]() 时
时![]() 成立.
成立.
故⑤正确.
综上,③⑤正确.
故选:B


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:
【题目】某网店经营各种儿童玩具,该网店老板发现该店经销的一种手腕可以摇动的![]() 款芭比娃娃玩具在某周内所获纯利
款芭比娃娃玩具在某周内所获纯利![]() (元)与该周每天销售这种芭比娃娃的个数
(元)与该周每天销售这种芭比娃娃的个数![]() (个)之间的关系如下表:
(个)之间的关系如下表:
每天销售芭比娃娃个数 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
该周内所获纯利 | 66 | 69 | 74 | 81 | 89 | 90 | 91 |
(1)由表中数据可推测![]() 线性相关,求出回归直线方程;
线性相关,求出回归直线方程;
(2)请你预测当该店每天销售这种芭比娃娃20件时,每周获纯利多少?
参考公式: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() = (1,2sinθ),
= (1,2sinθ),![]() = (sin(θ+
= (sin(θ+![]() ),1),θ
),1),θ![]() R。
R。
(1) 若![]() ⊥
⊥![]() ,求 tanθ的值;
,求 tanθ的值;
(2) 若![]() ∥
∥![]() ,且 θ
,且 θ![]() (0,
(0,![]() ),求 θ的值
),求 θ的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平行四边形![]() 中,
中,![]() ,
,![]() ,过
,过![]() 点作
点作![]() 的垂线,交
的垂线,交![]() 的延长线于点
的延长线于点![]() ,
,![]() .连结
.连结![]() ,交
,交![]() 于点
于点![]() ,如图1,将
,如图1,将![]() 沿
沿![]() 折起,使得点
折起,使得点![]() 到达点
到达点![]() 的位置,如图2.
的位置,如图2.
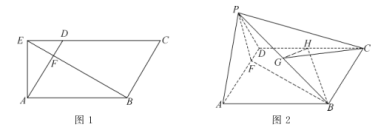
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,且平面
的中点,且平面![]() 平面
平面![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 是某景区的两条道路(宽度忽略不计,
是某景区的两条道路(宽度忽略不计,![]() 为东西方向),Q为景区内一景点,A为道路
为东西方向),Q为景区内一景点,A为道路![]() 上一游客休息区,已知
上一游客休息区,已知![]() ,
,![]() (百米),Q到直线
(百米),Q到直线![]() ,
,![]() 的距离分别为3(百米),
的距离分别为3(百米),![]() (百米),现新修一条自A经过Q的有轨观光直路并延伸至道路
(百米),现新修一条自A经过Q的有轨观光直路并延伸至道路![]() 于点B,并在B处修建一游客休息区.
于点B,并在B处修建一游客休息区.
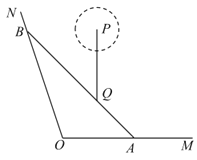
(1)求有轨观光直路![]() 的长;
的长;
(2)已知在景点Q的正北方6百米的P处有一大型组合音乐喷泉,喷泉表演一次的时长为9分钟,表演时,喷泉喷洒区域以P为圆心,r为半径变化,且t分钟时,![]() (百米)(
(百米)(![]() ,
,![]() ).当喷泉表演开始时,一观光车S(大小忽略不计)正从休息区B沿(1)中的轨道
).当喷泉表演开始时,一观光车S(大小忽略不计)正从休息区B沿(1)中的轨道![]() 以
以![]() (百米/分钟)的速度开往休息区A,问:观光车在行驶途中是否会被喷泉喷洒到,并说明理由.
(百米/分钟)的速度开往休息区A,问:观光车在行驶途中是否会被喷泉喷洒到,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com