
(本小题满分12分)
设数列 的各项都为正数,其前
的各项都为正数,其前 项和为
项和为 ,已知对任意
,已知对任意 ,
, 是
是 和
和 的等比中项.
的等比中项.
(Ⅰ)证明数列 为等差数列,并求数列
为等差数列,并求数列 的通项公式;
的通项公式;
(Ⅱ)证明 ;
;
(Ⅲ)设集合 ,
, ,且
,且 ,若存在
,若存在 ∈
∈ ,使对满足
,使对满足 的一切正整数
的一切正整数 ,不等式
,不等式 恒成立,求这样的正整数
恒成立,求这样的正整数 共有多少个?
共有多少个?
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源:2011届重庆市八中高三第二次月考理科数学卷 题型:解答题
(本小题满分12分)已知数列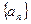 的首项为
的首项为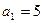 ,前
,前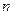 项和为
项和为 ,且
,且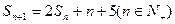
(1)求证:数列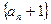 成等比数列;
成等比数列;
(2)令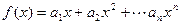 ,求函数
,求函数 在点
在点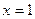 处的导数
处的导数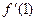 .
.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年重庆市高三第二次月考理科数学卷 题型:解答题
(本小题满分12分)已知数列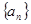 的首项为
的首项为 ,前
,前 项和为
项和为 ,且
,且
(1)求证:数列 成等比数列;
成等比数列;
(2)令 ,求函数
,求函数 在点
在点 处的导数
处的导数 .
.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年重庆市七区高三第一次调研测试数学理卷 题型:解答题
(本小题满分12分)
设数列 的各项都为正数,其前
的各项都为正数,其前 项和为
项和为 ,已知对任意
,已知对任意 ,
, 是
是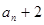 和
和 的等比中项.
的等比中项.
(Ⅰ)证明数列 为等差数列,并求数列
为等差数列,并求数列 的通项公式;
的通项公式;
(Ⅱ)证明 ;
;
(Ⅲ)设集合 ,
, ,且
,且 ,若存在
,若存在 ∈
∈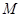 ,使对满足
,使对满足 的一切正整数
的一切正整数 ,不等式
,不等式 恒成立,求这样的正整数
恒成立,求这样的正整数 共有多少个?
共有多少个?
查看答案和解析>>
科目:高中数学 来源:2010-2011学年重庆市七区高三第一次调研测试数学理卷 题型:解答题
(本小题满分12分)
某地设计修建一条26公里长的轻轨交通路线,该轻轨交通路线的起点站和终点站已建好,余下工程只需要在该段路线的起点站和终点站之间修建轻轨道路和轻轨中间站,相邻两轻轨站之间的距离均为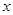 公里.经预算,修建一个轻轨中间站的费用为2000万元,修建
公里.经预算,修建一个轻轨中间站的费用为2000万元,修建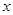 公里的轻轨道路费用为(
公里的轻轨道路费用为(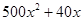 )万元.设余下工程的总费用为
)万元.设余下工程的总费用为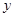 万元.
万元.
(Ⅰ)试将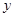 表示成
表示成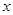 的函数;
的函数;
(Ⅱ)需要修建多少个轻轨中间站才能使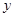 最小?其最小值为多少万元?
最小?其最小值为多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com