
(本小题满分14分)已知平行四边形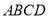 ,
, ,
,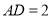 ,
, ,
,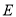 为
为 的中点,把三角形
的中点,把三角形 沿
沿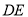 折起至
折起至 位置,使得
位置,使得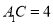 ,
,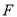 是线段
是线段 的中点.
的中点.

(1)求证: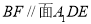 ;
;
(2)求证:面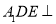 面
面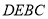 ;
;
(3)求二面角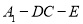 的正切值.
的正切值.
(1)证明见解析;(2)证明见解析;(3)2.
【解析】
试题分析:(1)此题将线面平行转化为线线平行问题,可取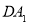 的中点
的中点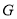 ,连接
,连接 构造辅助线,得到
构造辅助线,得到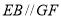 ,进而证明出
,进而证明出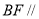 平面
平面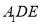 ;(2)此题将面面垂直问题转化为线面垂直问题,可取
;(2)此题将面面垂直问题转化为线面垂直问题,可取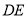 的中点
的中点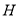 ,连接
,连接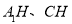 构造辅助线,借助于余弦定理,得出
构造辅助线,借助于余弦定理,得出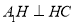 ,即
,即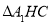 为直角三角形,由线面垂直的判定定理,证明出
为直角三角形,由线面垂直的判定定理,证明出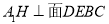 ,根据面面垂直的判定定理得出面
,根据面面垂直的判定定理得出面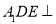 面
面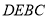 ;
;
(3)构造辅助线过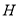 作
作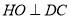 于
于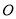 ,连接
,连接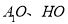 ,证明出
,证明出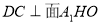 ,则
,则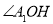 是二面角
是二面角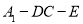 的平面角,计算即可求得.
的平面角,计算即可求得.
试题解析: (1) 如图

证明:取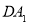 的中点
的中点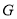 ,连接
,连接
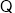
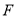 为
为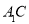 中点
中点

 ,且
,且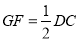
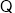
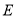 为平行四边形
为平行四边形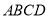 边
边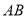 的中点
的中点

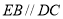 ,且
,且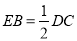

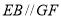 ,且
,且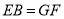
 四边形
四边形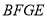 是平行四边形
是平行四边形

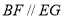
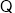
 平面
平面 ,
, 平面
平面

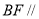 平面
平面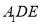 4分
4分
(2)取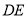 的中点
的中点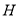 ,连接
,连接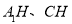

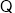
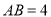 ,
, ,
,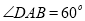 ,
,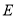 为
为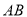 的中点
的中点

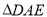 为等边三角形,即折叠后
为等边三角形,即折叠后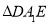 也为等边三角形
也为等边三角形

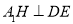 ,且
,且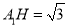
在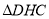 中,
中,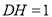 ,
,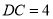 ,
,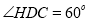
根据余弦定理,可得
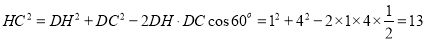 在
在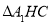 中,
中,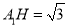 ,,
,,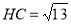
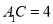 ,
,

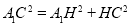 ,即
,即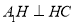

又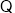
 ,所以
,所以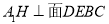
又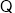
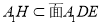
 面
面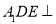 面
面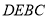 10分
10分
(3)过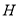 作
作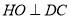 于
于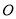 ,连接
,连接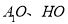
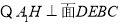
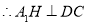
又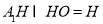
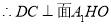
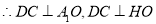

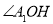 是二面角
是二面角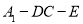 的平面角
的平面角
在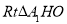 中,
中,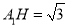 ,
,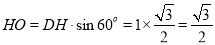 ,故
,故
所以二面角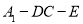 的正切值为
的正切值为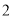 14分
14分
考点:1、线面平行;2、面面垂直;2、求二面角的三角函数值.


 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源:2014-2015学年广东省珠海市高三上学期期末考试文科数学试卷(解析版) 题型:选择题
若变量x,y满足约束条件 ,从可行域里任意取一点(x,y)则2x-y>0的概率为( ).
,从可行域里任意取一点(x,y)则2x-y>0的概率为( ).
A、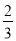 B、
B、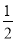 C、
C、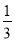 D、
D、
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省珠海市高三上学期期末考试文科数学试卷(解析版) 题型:选择题
已知复数z满足(3+i)z=i,则z=( ).
A、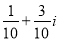 B、-
B、-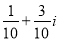 C、
C、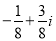 D、
D、
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省六校高三3月联考文科数学试卷(解析版) 题型:填空题
已知平面向量 =(sin2x, cos2x),
=(sin2x, cos2x),  =(sin2x, -cos2x), x∈R, f(x)=
=(sin2x, -cos2x), x∈R, f(x)= ·
· +4cos2x+2
+4cos2x+2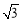 sinxcosx,如果m∈R, x∈R, f(x)≥f(m),则f(m)= .
sinxcosx,如果m∈R, x∈R, f(x)≥f(m),则f(m)= .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北省武汉市毕业生二月调研测试文科数学试卷(解析版) 题型:选择题
已知 是曲线
是曲线 上任意一点,
上任意一点, 为坐标原点,则
为坐标原点,则 的最小值为
的最小值为
A.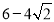 B.
B. C.
C. D.1
D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com