
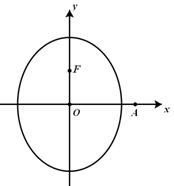
已知椭圆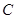 的对称中心为坐标原点,上焦点为
的对称中心为坐标原点,上焦点为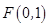 ,离心率
,离心率 .
.
(Ⅰ)求椭圆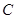 的方程;
的方程;
(Ⅱ)设 为
为 轴上的动点,过点
轴上的动点,过点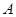 作直线
作直线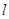 与直线
与直线 垂直,试探究直线
垂直,试探究直线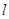 与椭圆
与椭圆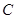 的位置关系.
的位置关系.
(Ⅰ) ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
【解析】
试题分析:(Ⅰ)先根据题中的已知条件以及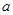 、
、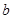 、
、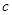 三者之间的关系求出
三者之间的关系求出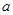 、
、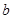 、
、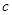 的值,从而确定椭圆
的值,从而确定椭圆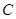 的方程;(Ⅱ)先根据直线
的方程;(Ⅱ)先根据直线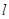 与直线
与直线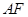 垂直这一条件确定直线
垂直这一条件确定直线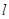 的方程(用点
的方程(用点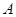 的横坐标表示),然后将直线
的横坐标表示),然后将直线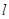 的方程联立转化成关于
的方程联立转化成关于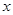 或
或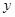 的一元二次方程,对
的一元二次方程,对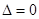 ,
,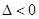 ,
,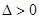 三种情况进行分类讨论,并确定相应的
三种情况进行分类讨论,并确定相应的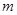 的取值范围.
的取值范围.
试题解析:(Ⅰ)由条件可知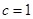 ,
,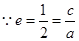 ,
,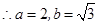 , 3分
, 3分
所以椭圆 的标准方程为
的标准方程为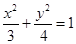 .
4分
.
4分
(Ⅱ)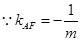 ,
,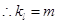 , 6分
, 6分
则直线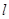 :
: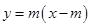 . 7分
. 7分
联立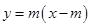 与
与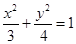
有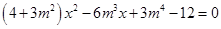 ,
9分
,
9分
则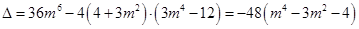
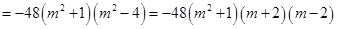 , 10分
, 10分
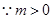 ,
,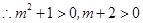 ,
,
则当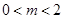 时,
时,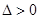 ,此时直线
,此时直线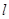 与椭圆
与椭圆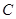 相交; 11分
相交; 11分
当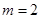 时,
时,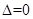 ,此时直线
,此时直线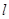 与椭圆
与椭圆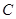 相切; 12分
相切; 12分
当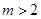 时,
时,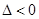 ,此时直线
,此时直线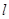 与椭圆
与椭圆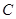 相离. 13分
相离. 13分
考点:椭圆的方程、直线与椭圆的位置关系


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案科目:高中数学 来源: 题型:
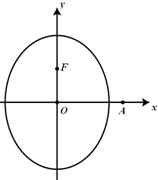 (2013•泉州模拟)已知椭圆C的对称中心为坐标原点,上焦点为F(0,1),离心率e=
(2013•泉州模拟)已知椭圆C的对称中心为坐标原点,上焦点为F(0,1),离心率e=| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(12分)已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() 的中心
的中心![]() 关于直线
关于直线![]() 的对称点落在直线
的对称点落在直线![]() 上
上
(1)求椭圆C的方程;
(2)设![]() 是椭圆
是椭圆![]() 上关于
上关于![]() 轴对称的任意两点,连接
轴对称的任意两点,连接![]() 交椭圆
交椭圆![]() 于另一点
于另一点![]() ,求直线
,求直线![]() 的斜率范围并证明直线
的斜率范围并证明直线![]() 与
与![]() 轴相交顶点。
轴相交顶点。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年内蒙古高三5月月考文科数学试卷(解析版) 题型:解答题
已知椭圆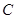 的对称中心为原点
的对称中心为原点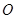 ,焦点在
,焦点在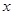 轴上,左、右焦点分别为
轴上,左、右焦点分别为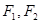 ,且
,且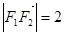 ,点
,点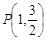 在该椭圆上.
在该椭圆上.
(1)求椭圆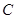 的方程;
的方程;
(2)过点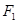 的直线
的直线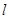 与椭圆
与椭圆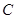 相交于
相交于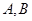 两点,若
两点,若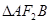 的面积为
的面积为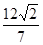 ,求以
,求以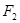 为圆心且与直线
为圆心且与直线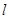 相切的圆的方程.
相切的圆的方程.
查看答案和解析>>
科目:高中数学 来源:2010年河北省冀州中学高二下学期期中考试数学(理) 题型:解答题
已知椭圆 的对称中心为原点O,焦点在
的对称中心为原点O,焦点在 轴上,离心率为
轴上,离心率为 ,且点(1,
,且点(1, )在该椭圆上.
)在该椭圆上.
(I)求椭圆 的方程;
的方程;
(II)过椭圆 的左焦点
的左焦点 的直线
的直线 与椭圆
与椭圆 相交于
相交于 两点,若
两点,若 的面积为
的面积为 ,求圆心在原点O且与直线
,求圆心在原点O且与直线 相切的圆的方
相切的圆的方 程. 高☆考♂资♀源?网
程. 高☆考♂资♀源?网
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com