
设数列{an}的首项不为零,前n项和为Sn,且对任意的r,t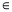 N*,都有
N*,都有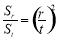 .
.
(1)求数列{an}的通项公式(用a1表示);
(2)设a1=1,b1=3,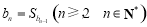 ,求证:数列
,求证:数列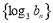 为等比数列;
为等比数列;
(3)在(2)的条件下,求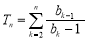 .
.
(1)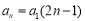 ;(2)详见解析;(3)
;(2)详见解析;(3) .
.
【解析】
试题分析:(1)根据题中所给数列递推关系的特征: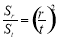 ,有且只有前n项和的比值,而题中又要求以a1表示,即可想到令
,有且只有前n项和的比值,而题中又要求以a1表示,即可想到令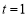 ,
,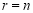 ,得到
,得到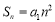 ,这样问题即可转化为由
,这样问题即可转化为由 求
求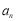 的问题,注意要分三步啊; (2)由(1)中所求
的问题,注意要分三步啊; (2)由(1)中所求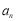 的表达式,并已知a1=1,即可确定出
的表达式,并已知a1=1,即可确定出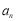 的通项公式和前n项和公式,再运用条件
的通项公式和前n项和公式,再运用条件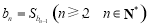 ,不难求出关系:
,不难求出关系: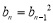 ,结合所证数列的特征和等比数列的定义,可得
,结合所证数列的特征和等比数列的定义,可得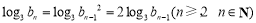 ,即可得证; (3)由在(2)的条件下,即可得出
,即可得证; (3)由在(2)的条件下,即可得出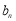 的通项公式:
的通项公式: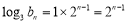 化简得
化简得 ,观察其特点和所求目标
,观察其特点和所求目标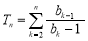 ,不难想到求出:
,不难想到求出: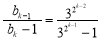 ,运用代数知识化简得:
,运用代数知识化简得: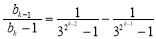 ,这样就可联想到数列求和中的裂项相消的方法,可得:
,这样就可联想到数列求和中的裂项相消的方法,可得: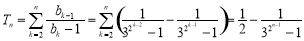 .
.
试题解析:(1)因为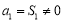 ,令
,令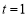 ,
,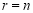 ,则
,则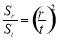 ,得
,得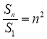 ,即
,即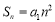 . 2分
. 2分
当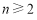 时,
时,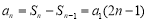 ,且当
,且当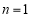 时,此式也成立.
时,此式也成立.
故数列{an}的通项公式为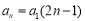 . 5分
. 5分
(2)当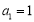 时,由(1)知
时,由(1)知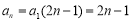 ,Sn=n2.
,Sn=n2.
依题意,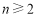 时,
时,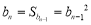 , 7分
, 7分
于是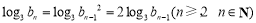 ,且
,且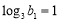 ,
,
故数列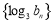 是首项为1,公比为2的等比数列. 10分
是首项为1,公比为2的等比数列. 10分
(3)由(2)得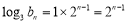 ,所以
,所以 . 12分
. 12分
于是 . 15分
. 15分
所以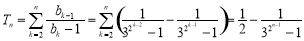 . 16分
. 16分
考点:1.递推关系的处理;2.等比数列的定义;3.数列求和的应用


科目:高中数学 来源:2013-2014学年江苏省徐州市高三第三次质量检测理科数学试卷(解析版) 题型:填空题
从高三年级随机抽取100名学生,将他们的某次考试数学成绩绘制成频率分布直方图.由图中数据可知成绩在[130,140)内的学生人数为 .
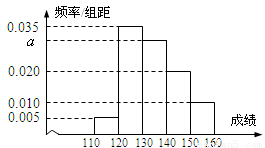
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省南通市高三年级第三次模拟考试理科数学试卷(解析版) 题型:解答题
在△ABC中,角A,B,C所对的边分别为a,b,c.若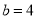 ,
,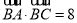 .
.
(1)求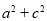 的值;
的值;
(2)求函数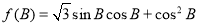 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省南京市高三年级第三次模拟考试数学试卷(解析版) 题型:解答题
已知圆O的内接△ABC中,D为BC上一点,且△ADC为正三角形,点E为BC的延长线上一
点,AE为圆O的切线,求证:CD2=BD·EC.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com