
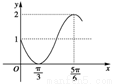
设函数y=sin(ωx+φ)+1(ω>0)的一段图象如右图所示,则周期T、初相φ的值依次为( )
A.π,-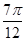 B.2π,
B.2π,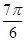
C.π,-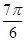 D.2π,-
D.2π,-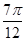
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:贵州省湄潭中学2012届高三第四次月考数学文科试题 题型:013
设ω>0,函数y=sin(ωx+![]() )+2的图像向右平移
)+2的图像向右平移![]() 个单位后与原图像重合,则ω的最小值是
个单位后与原图像重合,则ω的最小值是
![]()
![]()
![]()
3
查看答案和解析>>
科目:高中数学 来源:北京市石景山区2008-2009学年高三第一学期期末考试数学(文科)试题 题型:022
设函数f(x)的图象与直线x=a,x=b及x轴所围成图形的面积称为函数f(x)在[a,b]上的面积,已知函数y=sinx在[0,![]() ]上的面积为
]上的面积为![]() (n∈N*),则
(n∈N*),则
(1)函数y=sin3x在[0,![]() ]上的面积为________;
]上的面积为________;
(2)函数y=sin(3x-π)+1在[![]() ,
,![]() ]上的面积为________.
]上的面积为________.
查看答案和解析>>
科目:高中数学 来源:2014届山东省日照市高三上学期第一次月考理科数学试卷(解析版) 题型:解答题
设函数f(θ)= sinθ+cosθ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
sinθ+cosθ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
(1)若点P的坐标为 ,求f(θ)的值;
,求f(θ)的值;
(2)若点P(x,y)为平面区域Ω: ,上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
,上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
下列三种说法:
①命题“![]() x∈R,使得x2+1>3x”的否定是“
x∈R,使得x2+1>3x”的否定是“![]() x∈R,都有x2+1≤3x”;
x∈R,都有x2+1≤3x”;
②设p、q是简单命题,若“p∨q”为假命题,则“![]() p∧
p∧![]() q”为真命题;
q”为真命题;
③把函数y=sin(-2x)(x∈R)的图象上所有的点都向右平移![]() 个单位即可得到函数y=sin(
个单位即可得到函数y=sin(![]() )(x∈R)的图象.其中正确说法的序号是_________.
)(x∈R)的图象.其中正确说法的序号是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com