
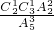 =
= .
.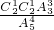
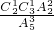 +
+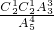 =
= .
.

科目:高中数学 来源: 题型:解答题
 =(sinA,cos2A),
=(sinA,cos2A), =(2cosA,1),f(A)=
=(2cosA,1),f(A)= •
• ,求f(A)取得最大值和最小值时A的值.
,求f(A)取得最大值和最小值时A的值.查看答案和解析>>
科目:高中数学 来源: 题型:单选题
| 男 | 女 | 总计 | |
| 爱好 | 10 | 40 | 50 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 30 | 70 | 100 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 |
| k | 2.706 | 3.841 | 5.024 |
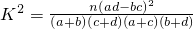 ,经计算,统计量K2的观测值k≈4.762,参照附表,得到的正确结论是
,经计算,统计量K2的观测值k≈4.762,参照附表,得到的正确结论是查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 |的最小正周期是π;
|的最小正周期是π; x的图象的对称中心是(kπ,0),k∈Z;
x的图象的对称中心是(kπ,0),k∈Z; ),k∈Z;
),k∈Z; )的图象可由函数y=3sin2x的图象向右平移
)的图象可由函数y=3sin2x的图象向右平移 平移得到.
平移得到.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com