练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．已知a，b是常数，ab≠0，若函数f（x）=ax3+barcsinx+3的最大值为10，则f（x）的最小值为-4．

    分析 记函数g（x）=ax3+barcsinx，由函数的奇偶性和最值的关系可得．

    解答 解：记函数g（x）=ax3+barcsinx，
    ∵g（-x）=-ax3-barcsinx=-g（x），∴函数g（x）为奇函数，
    设当x=x0时，函数f（x）=ax3+barcsinx+3的最大值为10，
    则f（x0）=ax03+barcsinx0+3=10，此时g（x）取最大值g（x0）=7，
    由奇函数的性质可得当x=-x0时，函数g（x）取最小值g（-x0）=-7，
    ∴当x=-x0时，函数f（x）取最小值-7+3=-4，
    故答案为：-4．

    点评 本题考查三角函数的最值，涉及函数的奇偶性和最值，属中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    4．已知三棱锥P-ABC，在底面△ABC中，∠A=60°，$BC=\sqrt{3}$，PA⊥面ABC，PA=2，则此三棱锥的外接球的体积为（　　）
    A．$\frac{{8\sqrt{2}}}{3}π$B．$4\sqrt{3}π$C．$\frac{{4\sqrt{2}π}}{3}$D．8π

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．用数字1、2、3、4、5组成无重复数字的三位数，其中奇数的个数为36．（结果用数值表示）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．已知数列{an}是等差数列，且S3=6，a3=0，则它的公差d=-2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．设向量$\overrightarrow{a}$=（3，3），$\overrightarrow{b}$=（1，-1），若（$\overrightarrow{a}$+λ$\overrightarrow{b}$）⊥（$\overrightarrow{a}$-λ$\overrightarrow{b}$），则实数λ=（　　）
    A．3B．1C．±1D．±3

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

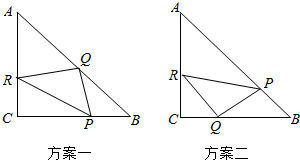    19．在一个直角边长为10m的等腰直角三角形ABC的草地上，铺设一个也是等腰直角三角形PQR的花地，要求P，Q，R三点分别在△ABC的三条边上，且要使△PQR的面积最小，现有两种设计方案：
    方案-：直角顶点Q在斜边AB上，R，P分别在直角边AC，BC上；
    方案二：直角顶点Q在直角边BC上，R，P分别在直角边AC，斜边AB上．请问应选用哪一种方案？并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知数列{an}是公差不为0的等差数列，a1=$\frac{1}{2}$，数列{bn}是等比数列，且b1=a1，b2=a3，b3=a4，数列{bn}的前n项和为Sn．记点Qn（bn，Sn），n∈Z+．
    （1）求数列{an}，{bn}的通项公式；
    （2）证明点Q1，Q2，Q3，…，Qn…在同一条直线l上，并求出直线l的方程；
    （3）若△OQnQn+1，（n∈Z+）的面积为An，Tn为数列{An}的前n项和之和，求：$\underset{lim}{n→∞}$An及$\underset{lim}{n→∞}$Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．设命题p：?x＞1，x2+1＞2，则￢p为（　　）
    A．?x＞1，x2+1≤2B．?x＞1，x2+1≤2C．?x≤1，x2+1≤2D．?x≤1，x2+1≤2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．在△ABC中，a、b、c分别为角A、B、C的对边，4sin2$\frac{B+C}{2}$-cos2A=$\frac{7}{2}$，求角A的度数．

    查看答案和解析>>

    同步练习册答案