
等差数列{an}的奇数项的和为216,偶数项的和为192,首项为1,项数为奇数,求此数列的末项和通项公式.
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
| S10 |
| 10 |
| S100 |
| 100 |
| S110 |
| 110 |
| 1 |
| x |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| lnx |
| 3 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)如果命题P:“x>2”是真命题,则Q:“x≥2”是真命题;
(2)函数f(x)=x-![]() 是奇函数,且在(-1,0)∪(0,1)上是增函数;
是奇函数,且在(-1,0)∪(0,1)上是增函数;
(3)“a≠1且b≠1”的充分不必要条件是“(a-1)2+(b-1)2≠0”;
(4)如果等差数列{an}的前n项的和是Sn,等比数列{bn}的前n项的和是Tn,则Sk,S2k-Sk,S3k-S2k成等差数列,Tk,T2k-Tk,T3k-T2k成等比数列.
其中正确命题的序号是:_______________________.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 ),(100,
),(100, ),(110,
),(110,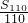 ),共线;
),共线; +k在(0,1)没有零点,则k的取值范围是k≥2,
+k在(0,1)没有零点,则k的取值范围是k≥2, ,则xf(x)<1的解集为(-2,2).
,则xf(x)<1的解集为(-2,2).查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| S10 |
| 10 |
| S100 |
| 100 |
| S110 |
| 110 |
| 1 |
| x |
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com