
(2014•安徽模拟)若2m+4n<2 ,则点(m,n)必在( )
,则点(m,n)必在( )
A.直线x+y=1的左下方 B.直线x+y=1的右上方
C.直线x+2y=1的左下方 D.直线x+2y=1的右上方
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源:[同步]2014年新人教A版选修4-5 2.2综合法与分析法练习卷(解析版) 题型:选择题
关于综合法和分析法说法错误的是( )
A.综合法和分析法是直接证明中最基本的两种证明方法
B.综合法又叫顺推证法或由因导果法
C.分析法又叫逆推证法或执果索因法
D.综合法和分析法都是因果分别互推的两头凑法
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 1.2绝对值不等式练习卷(解析版) 题型:选择题
(2014•江西二模)若存在x∈R,使|2x﹣a|+2|3﹣x|≤1成立,则实数a的取值范围是( )
A.[2,4] B.(5,7) C.[5,7] D.(﹣∞,5]∪[7,+∞)
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 1.1不等式练习卷(解析版) 题型:选择题
(2014•鹤城区二模)已知a,b为正实数,函数y=2aex+b的图象经过点(O,1),则 的最小值为( )
的最小值为( )
A.3+2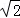 B.3﹣2
B.3﹣2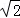 C.4 D.2
C.4 D.2
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 1.1不等式练习卷(解析版) 题型:选择题
(2014•咸阳二模)若正实数a,b满足a+b=1,则( )
A.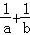 有最大值4 B.ab有最小值
有最大值4 B.ab有最小值
C.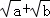 有最大值
有最大值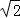 D.a2+b2有最小值
D.a2+b2有最小值
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-4 1.4柱坐标系与球坐标系简介(解析版) 题型:选择题
已知点P1的球坐标是P1(4,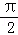 ,
,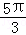 ),P2的柱坐标是P2(2,
),P2的柱坐标是P2(2,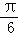 ,1),则|P1P2|=( )
,1),则|P1P2|=( )
A.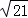 B.
B.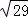 C.
C.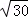 D.
D.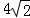
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 3.3逆矩阵与二元一次方程组(解析版) 题型:选择题
(2012•闵行区一模)已知关于x,y的二元一次线性方程组的增广矩阵为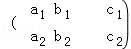 ,记
,记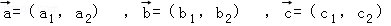 ,则此线性方程组有无穷多组解的充要条件是( )
,则此线性方程组有无穷多组解的充要条件是( )
A.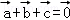 B.
B.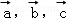 两两平行
两两平行
C.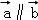 D.
D.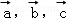 方向都相同
方向都相同
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com