
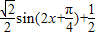 ,由2kπ+
,由2kπ+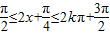 ,k∈Z,解得x的范围即为所求.
,k∈Z,解得x的范围即为所求.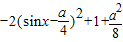 ,分
,分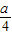 >1、
>1、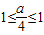 、
、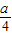 <-1三种情况分别根据其最大值
<-1三种情况分别根据其最大值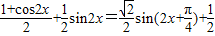 ,
,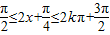 ,k∈Z,解得
,k∈Z,解得 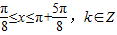 ,
,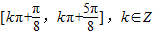 .
.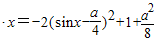 ,
, >1,即a>4时,则sinx=1时有最大值,∴-1+a=1,∴a=2,(舍去).
>1,即a>4时,则sinx=1时有最大值,∴-1+a=1,∴a=2,(舍去).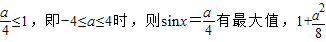 =1,∴a=0,合乎题意.
=1,∴a=0,合乎题意.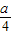 <-1,即a<-4时,怎sinx=-1有最大值.-1-a=1⇒a=-2,(舍去).
<-1,即a<-4时,怎sinx=-1有最大值.-1-a=1⇒a=-2,(舍去).

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:
|
| α |
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com