
分析 (1)设x∈[-2,0],则-x∈[0,2],结合函数的奇偶性,从而求出函数的解析式;
(2)由题意得g(x)max<f(x)min,分别求出g(x)的最大值和f(x)的最小值,得到关于a的不等式,从而求出a的范围.
解答 解:(1)设x∈[-2,0],则-x∈[0,2],
∵f(x)定义x∈[-2,2]是偶函数,
∴f(-x)=x+2$\sqrt{3+x}$,
∵f(-x)=f(x),∴f(x)=x+2$\sqrt{3+x}$,
∴f(x)=$\left\{\begin{array}{l}{x+2\sqrt{3+x},x∈[-2,0)}\\{-x+2\sqrt{3-x},x∈[0,2]}\end{array}\right.$;
(2)因为对任意x1,x2∈[-2.,2],都有g(x1)<f(x2)成立,
所以g(x)max<f(x)min,
又因为f(x)是定义在[-2,2]上的偶函数,
∴f(x)在区间[-2,0]和区间[0,2]上的值域相同.
当x∈[-2,0]时:f(x)=x+2$\sqrt{3+x}$,
设t=$\sqrt{3+x}$,则t∈[1,$\sqrt{3}$],
函数化为:y=t2+t-3,t∈[1,$\sqrt{3}$],
则f(x)min=-1,
又g(x)max=g(2)=a-2,
∴a-2<-1,∴a<1,
故a的范围是:0<a<1.
点评 本题考查了求函数的解析式问题,考查函数的奇偶性、函数恒成立问题,是一道中档题.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
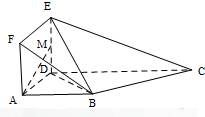 如图所示,已知多面体ABCDEF,平面ADEF⊥平面ABCD,ADEF为正方形,ABCD为直角梯形,且AB∥CD,AB⊥AD,AB=AD=$\frac{1}{2}$CD=1,M为线段ED上的动点.
如图所示,已知多面体ABCDEF,平面ADEF⊥平面ABCD,ADEF为正方形,ABCD为直角梯形,且AB∥CD,AB⊥AD,AB=AD=$\frac{1}{2}$CD=1,M为线段ED上的动点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com