练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    过△ABC的中线AD的中点E作直线PQ分别交AB、AC于P、Q两点，若
    AP
    =m
    AB
    ，
    AQ
    =n
    AC
    ，则
    1
    m
    +
    1
    n
    =（　　）
    分析：由D为BC的中点可知，
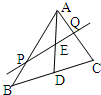
    AD
    =
    AB
    +
    BD
    =
    1
    2
    (
    AB
    +
    AC
    )    ，
    AE
    =
    1
    2
    (
    AP
    +
    AQ
    )    =
    1
    2
    m
    AB
     +
    1
    2
    n
    AC
    及
    AE
     =
    1
    2
    AD
    ，结合
    AB
    与
    AC
    不共线可得关于m，n的方程，从而可求m，n，进而可求
    解答：解：由D为BC的中点可知，
    AD
    =
    AB
    +
    BD
    =
    AB
    +
    1
    2
    BC
    =
    AB
    +
    1
    2
    (
    AC
    -
    AB
    )
    =
    1
    2
    (
    AB
    +
    AC
    )
    ∵
    AP
    =m
    AB
    ，
    AQ
    =n
    AC
    ，
    ∴
    AE
    =
    1
    2
    (
    AP
    +
    AQ
    )    =
    1
    2
    m
    AB
     +
    1
    2
    n
    AC

    ∵
    AE
     =
    1
    2
    AD

    ∴
    1
    2
    m
    AB
     +
    1
    2
    n
    AC
    =
    AB
    +
    AC
    4

    ∴(
    1
    2
    m-
    1
    4
    )
    AB
    =(
    1
    4
    -
    1
    2
    n)
    AC

    ∵
    AB
    与
    AC
    不共线
    ∴
    1
    2
    m-
    1
    4
    =0    ，
    1
    4
    -
    1
    2
    n=0
    ∴m=n=
    1
    2
    ，
    1
    m
    +
    1
    n
    =4
    故选A
    点评：本题主要考查了向量的基本运算的应用，向量的基本定理的应用及向量共线定理等知识的综合应用．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

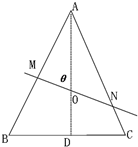    如图点O是边长为1的等边三角形ABC的边BC中线AD上一点，且|AO|=2|OD|，过O的直线交边AB于M，交边AC于N，记∠AOM=θ，
    （1）则θ的取值范围为
    [
    π
    3
    ，
    2π
    3
    ]
    [
    π
    3
    ，
    2π
    3
    ]

    （2）
    1
    |OM|2
    +
    1
    |ON|2
    的最小值为
    15
    15
    ．

    查看答案和解析>>

    科目：高中数学 来源：江西省南昌市2012届高三调研测试数学文科试题 题型：044

    如图M为的△ABC的中线AD的中点，过M的直线分别与边AB，AC交于点P，Q，设＝x，＝y记y＝f(x)

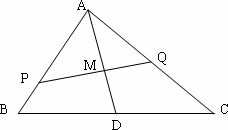
    (1)求函数y＝f(x)的表达式；

    (2)设g(x)＝x3＋3a2x＋2a，(x∈[0，1])，若对于任意x1∈[，1]，总存在x2∈[0，1]使得f(x1)＝g(x2)成立，求实数a的取值范围；

    查看答案和解析>>

    科目：高中数学 来源：江西省南昌市2012届高三调研测试数学理科试题 题型：044

    如图M为的△ABC的中线AD的中点，过M的直线分别与边AB，AC交于点P，Q，设＝x，＝y，记y＝f(x)

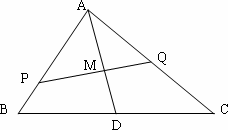
    (1)求函数y＝f(x)的表达式；

    (2)设g(x)＝x3＋3a2x＋2a，(x∈[0，1])，若对于任意x1∈[，1]，总存在x2∈[0，1]使得f(x1)＝g(x2)成立，求实数a的取值范围；

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    过△ABC的中线AD的中点E作直线PQ分别交AB、AC于P、Q两点，若数学公式，则数学公式=


    1. A.
      4
    2. B.
      数学公式
    3. C.
      3
    4. D.
      1

    查看答案和解析>>

    同步练习册答案