
【题目】己知椭圆: ![]() 上动点PQ,O为原点;
上动点PQ,O为原点;
(1)若![]() ,求证:
,求证:![]() 为定值;
为定值;
(2)点![]() ,若
,若![]() ,求证:直线
,求证:直线![]() 过定点;
过定点;
(3)若![]() ,求证:直线
,求证:直线![]() 为定圆的切线;
为定圆的切线;
【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析
【解析】
(1)设![]() ,由题意可知
,由题意可知![]() ,将
,将![]() 代入椭圆方程,求得
代入椭圆方程,求得![]() ,利用直线的斜率公式,即可求证
,利用直线的斜率公式,即可求证![]() 为定值;
为定值;
(2)将直线方程代入椭圆方程,利用韦达定理及直线的斜率公式,即可求得![]() 的值,则直线
的值,则直线![]() 过定点;
过定点;
(3)设![]() ,则
,则![]() 方程为:
方程为:![]() ,分别代入椭圆方程,利用韦达定理及三角形的性质,
,分别代入椭圆方程,利用韦达定理及三角形的性质,![]() 到直线
到直线![]() 的距离
的距离![]() 为定值,即可求得直线
为定值,即可求得直线![]() 为定圆
为定圆![]()
的切线,再验证![]() 中有一个斜率不存在的情况即可.
中有一个斜率不存在的情况即可.
证明:(1)由题意可知:设![]() ,
,
![]() ,
,
由![]() 在椭圆上,则
在椭圆上,则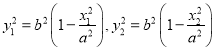 ,
,
代入得: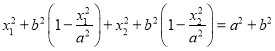
整理得:![]() ,
,
则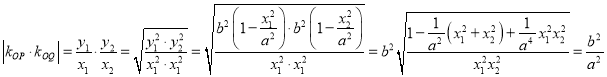
∴![]() 为定值
为定值![]() ;
;
(2)易知,直线![]() 的斜率存在,设其方程为
的斜率存在,设其方程为![]() ,设
,设![]() ,
,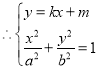 ,消去
,消去![]() ,整理得
,整理得![]() ,
,
则 ![]() ,
,
由![]() ,且直线
,且直线![]() 的斜率均存在,
的斜率均存在,![]() ,整理得
,整理得![]() ,
,
因为![]() ,
,
所以![]() ,
,
整理得![]() ,
,![]() .
.
解得![]() ,或
,或![]() (舍去).
(舍去).
∴直线![]() 恒过定点
恒过定点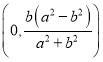 ;
;
(3)当![]() 斜率都存在时,
斜率都存在时,
设![]() 方程为:
方程为:![]() ,
,![]() ,
,
则![]() 方程为:
方程为:![]() ,
,
联立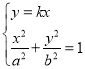 ,可得:
,可得:![]() ,
,![]() ,
,
同理可得:![]()
则![]() 到直线
到直线![]() 的距离
的距离![]() ,即为
,即为![]() 斜边上的高,
斜边上的高,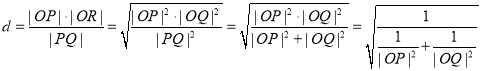
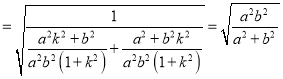 ,(定值).
,(定值).
当![]() 的斜率有一个不存在时,
的斜率有一个不存在时,
此时直线![]() 为连接长轴和短轴端点的一条直线,方程为
为连接长轴和短轴端点的一条直线,方程为![]() ,
,
圆心![]() 到其距离为
到其距离为![]() ,
,
综合得:直线![]() 为定圆
为定圆![]() 的切线.
的切线.


科目:高中数学 来源: 题型:
【题目】折纸与数学有着千丝万缕的联系,吸引了人们的广泛兴趣.因![]() 纸的长宽比
纸的长宽比![]() 称为白银分割比例,故
称为白银分割比例,故![]() 纸有一个白银矩形的美称.现有一张如图1所示的
纸有一个白银矩形的美称.现有一张如图1所示的![]() 纸
纸![]() ,
,![]() .
.
![]() 分别为
分别为![]() 的中点,将其按折痕
的中点,将其按折痕![]() 折起(如图2),使得
折起(如图2),使得![]() 四点重合,重合后的点记为
四点重合,重合后的点记为![]() ,折得到一个如图3所示的三棱锥
,折得到一个如图3所示的三棱锥![]() .记
.记![]() 为
为![]() 的中点,在
的中点,在![]() 中,
中,![]() 为
为![]() 边上的高.
边上的高.
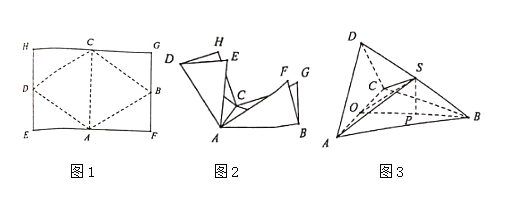
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() 分别是棱
分别是棱![]() 上的动点,且
上的动点,且![]() .当三棱锥
.当三棱锥![]() 的体积最大时,求平面
的体积最大时,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别为△ABC三个内角A,B,C的对边,且acos C+![]() asin C-b-c=0.
asin C-b-c=0.

(1)求A;
(2)若AD为BC边上的中线,cos B=![]() ,AD=
,AD=![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线C:y2=4x的焦点为F,过F的直线l与C交于A,B两点,点M的坐标为(﹣1,0).
(1)当l与x轴垂直时,求△ABM的外接圆方程;
(2)记△AMF的面积为S1,△BMF的面积为S2,当S1=4S2时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点Q是圆![]() 上的动点,点
上的动点,点![]() ,若线段QN的垂直平分线MQ于点P.
,若线段QN的垂直平分线MQ于点P.
(I)求动点P的轨迹E的方程
(II)若A是轨迹E的左顶点,过点D(-3,8)的直线l与轨迹E交于B,C两点,求证:直线AB、AC的斜率之和为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年,在庆祝中华人民共和国成立
年,在庆祝中华人民共和国成立![]() 周年之际,又迎来了以“创军人荣耀,筑世界和平”为宗旨的第七届世界军人运动会.据悉,这次军运会将于
周年之际,又迎来了以“创军人荣耀,筑世界和平”为宗旨的第七届世界军人运动会.据悉,这次军运会将于![]() 年
年![]() 月
月![]() 日至
日至![]() 日在美丽的江城武汉举行,届时将有来自全世界
日在美丽的江城武汉举行,届时将有来自全世界![]() 多个国家和地区的近万名军人运动员参赛.相对于奥运会、亚运会等大型综合赛事,军运会或许对很多人来说还很陌生.为此,武汉某高校为了在学生中更广泛的推介普及军运会相关知识内容,特在网络上组织了一次“我所知晓的武汉军运会”知识问答比赛,为便于对答卷进行对比研究,组委会抽取了
多个国家和地区的近万名军人运动员参赛.相对于奥运会、亚运会等大型综合赛事,军运会或许对很多人来说还很陌生.为此,武汉某高校为了在学生中更广泛的推介普及军运会相关知识内容,特在网络上组织了一次“我所知晓的武汉军运会”知识问答比赛,为便于对答卷进行对比研究,组委会抽取了![]() 名男生和
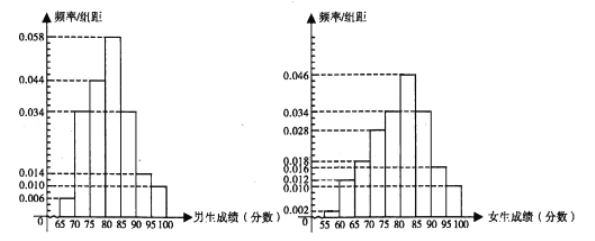
名男生和![]() 名女生的答卷,他们的考试成绩频率分布直方图如下:
名女生的答卷,他们的考试成绩频率分布直方图如下:
(注:问卷满分为![]() 分,成绩
分,成绩![]() 的试卷为“优秀”等级)
的试卷为“优秀”等级)
(1)从现有![]() 名男生和
名男生和![]() 名女生答卷中各取一份,分别求答卷成绩为“优秀”等级的概率;
名女生答卷中各取一份,分别求答卷成绩为“优秀”等级的概率;
(2)求列联表中![]() ,
,![]() ,
,![]() ,
,![]() 的值,并根据列联表回答:能否在犯错误的概率不超过
的值,并根据列联表回答:能否在犯错误的概率不超过![]() 的前提下认为“答卷成绩为优秀等级与性别有关”?
的前提下认为“答卷成绩为优秀等级与性别有关”?
男 | 女 | 总计 | |
优秀 |
|
|
|
非优秀 |
|
|
|
总计 |
|
|
|
(3)根据男、女生成绩频率分布直方图,对他们的成绩的优劣进行比较.
附:参考公式:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对在直角坐标系的第一象限内的任意两点![]() ,
,![]() 作如下定义:
作如下定义:![]() ,那么称点
,那么称点![]() 是点
是点![]() 的“上位点”,同时点
的“上位点”,同时点![]() 是点
是点![]() 的“下位点”.
的“下位点”.
(1)试写出点![]() 的一个“上位点”坐标和一个“下位点”坐标;
的一个“上位点”坐标和一个“下位点”坐标;
(2)设![]() 、
、![]() 、
、![]() 、
、![]() 均为正数,且点
均为正数,且点![]() 是点
是点![]() 的上位点,请判断点
的上位点,请判断点![]() 是否既是点
是否既是点![]() 的“下位点”又是点
的“下位点”又是点![]() 的“上位点”,如果是请证明,如果不是请说明理由;
的“上位点”,如果是请证明,如果不是请说明理由;
(3)设正整数![]() 满足以下条件:对任意实数
满足以下条件:对任意实数![]() ,总存在
,总存在![]() ,使得点
,使得点![]() 既是点
既是点![]() 的“下位点”,又是点
的“下位点”,又是点![]() 的“上位点”,求正整数
的“上位点”,求正整数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列![]() 的公差
的公差![]() ,前
,前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
,![]()
(1)试寻找一个等差数列![]() 和一个非负常数
和一个非负常数![]() ,使得等式
,使得等式![]() 对于任意的正整数
对于任意的正整数![]() 恒成立,并说明你的理由;
恒成立,并说明你的理由;
(2)对于(1)中的等差数列![]() 和非负常数
和非负常数![]() ,试求
,试求![]() (
(![]() )的最大值.
)的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com