Question

若直线l过点(-3，-

3

2

)且被圆x²+y²=25截得的弦长为8，则直线l的方程是（　　）

• A．x=-3
• B．x=-3或y=-

  3

  2

• C．3x+4y+15=0
• D．x=-3或3x+4y+15=0

Answer 1

分析：由圆的方程得到圆的圆心坐标和半径，再结合直线被圆截得的弦长等于8求出圆心到直线的距离，然后分直线的斜率存在和不存在求解直线方程，斜率不存在时直接得答案，斜率存在时由点到直线的距离公式求解．

解答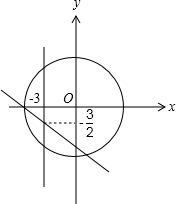：解：如图，
∵圆x²+y²=25的半径为5，直线l被圆截得的半弦长为4，∴圆心到直线的距离为3．
当直线l过点(-3，-

3

2

)且斜率不存在时，直线方程为x=-3，满足题意；
当斜率存在时，设斜率为k，则直线的点斜式方程为y+

3

2

=k(x+3)，
整理得：2kx-2y+6k-3=0．
由圆心（0，0）到直线2kx-2y+6k-3=0的距离等于3得：

|6k-3|

4k2+4

=3，解得：k=-

3

4

．
∴直线方程为3x+4y+15=0．
综上，直线l的方程是x=-3或3x+4y+15=0．
故选：D．

点评：本题考查了直线与圆的位置关系，考查了分类讨论的数学思想方法，具体方法是由圆心到直线的距离列式求解，是中档题．