
分析 (1)令x=1得出(1-2x)7=a0+a1+a2+…+a7=-1,x=0得出a0=1,即可求出a1+a2+…+a7;
(2)令x=1得出a0+a1+a2+…+a7=-1①,x=-1得出${a_0}-{a_1}+{a_2}-{a_3}+{a_4}-{a_5}+{a_6}-{a_7}={3^7}$②;
再对${({{a_0}+{a_2}+{a_4}+{a_6}})^2}-{({{a_1}+{a_3}+{a_5}+{a_7}})^2}$分解因式.
解答 解:(1)当x=1时,(1-2x)7=(1-2)7=-1,
展开式变为a0+a1+a2+…+a7=-1,
当x=0时,a0=1,
∴a1+a2+…+a7=-1-1=-2;
(2)由展开式知:a1,a3,a5,a7均为负,
a0,a2,a4,a6均为正;
令x=1,a0+a1+a2+…+a7=-1①,
令x=-1,${a_0}-{a_1}+{a_2}-{a_3}+{a_4}-{a_5}+{a_6}-{a_7}={3^7}$②;
∴${({{a_0}+{a_2}+{a_4}+{a_6}})^2}-{({{a_1}+{a_3}+{a_5}+{a_7}})^2}$
=(a0+a1+a2+a3+a4+a5+a6+a7)(a0-a1+a2-a3+a4-a5+a6-a7)
=-1×37
=-37.
点评 本题考查了用特殊值求多项式系数的应用问题,也考查了整体思想与因式分解的应用问题,是基础题目.


科目:高中数学 来源: 题型:选择题
| A. | $2{cos^2}\frac{π}{12}-1$ | B. | $\frac{{2tan{{22.5}°}}}{{1-{{tan}^2}{{22.5}°}}}$ | ||
| C. | 1-2sin275° | D. | sin15°cos15° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
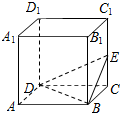
| A. | BD⊥A1C1 | B. | AC1∥平面BDE | ||
| C. | 平面BDE∥平面AB1D1 | D. | 平面A1BD⊥平面BDE |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com