
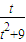 ≤a≤
≤a≤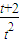 在t∈(0,
在t∈(0,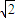 ]上恒成立,则a的取值范围是 .
]上恒成立,则a的取值范围是 .  ,g(t)=
,g(t)= ,t∈(0,
,t∈(0, ],利用基本不等式可求得f(t)max,g(t)min,从而可得答案.
],利用基本不等式可求得f(t)max,g(t)min,从而可得答案. ],令f(t)=
],令f(t)= ,g(t)=
,g(t)= ,
, =
=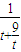 ,∵t+
,∵t+ 在(0,3]上单调递减,(0,
在(0,3]上单调递减,(0, ]?(0,3],
]?(0,3], 在(0,
在(0, ]上单调递减,
]上单调递减, ]上单调递增,
]上单调递增, )=
)=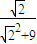 =
= ;
; =
= 在(0,
在(0, ]上单调递减,
]上单调递减, )=
)= .
. ≤a≤
≤a≤ .
. ,
, ].
].

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
已知不等式x2–3x+t<0的解集为{x|1<x<m, m??R}
(1)求t, m的值;
(2)若f(x)= –x2+ax+4在(–∞,1)上递增,求不等式log a (–mx2+3x+2–t)<0的解集。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省、金陵中学、南京外国语学校高三三校联考数学卷 题型:解答题
A.选修4-1:几何证明选讲
|
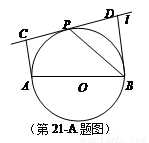
如图,设AB为⊙O的任一条不与直线l垂直的直径,P是⊙O与l的公共点,AC⊥l,BD⊥l,垂足分别为C,D,且PC=PD.求证:(1)l是⊙O的切线;(2)PB平分∠ABD.
B.选修4-2:矩阵与变换
(本小题满分10分)
已知点A在变换:T:→=作用后,再绕原点逆时针旋转90°,得到点B.若点B坐标为(-3,4),求点A的坐标.
C.选修4-4:坐标系与参数方程
(本小题满分10分)
求曲线C1:被直线l:y=x-所截得的线段长.
D.选修4-5:不等式选讲
(本小题满分10分)
已知a、b、c是正实数,求证:≥.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com